Top Links
Journal of Biostatistics and Biometric Applications
ISSN: 2455-765X
Genetic Algorithm and Ensemble Systems for Multi-biometric Cancellable Recognition
Copyright: © 2015 Canuto AMP. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Related article at Pubmed, Google Scholar
Biometrics usually provides several advantages over traditional forms of identity authentication. However, there are some concerns about the security of personal biometric data, while these systems need to ensure their integrity and public acceptance. The idea of cancellable biometrics has been introduced to overcome these security concerns. In addition, an important way to increase security and performance in biometric systems is the multi-biometric approach, which combines different sources of biometric information. This paper investigates the benefits that optimized ensemble systems and cancellable transformation functions can provide to multibiometric authentication systems. The main aim of the work reported here is to provide more security and better performance in the multi-biometric authentication process. We use as examples two different biometric modalities (face and voice) separately and in the multi-modal context (multi-biometric). The datasets used in this analysis were TIMIT for voice and the AR Face dataset for Face. As a result of this analysis, we will observe that the use of cancellable transformations in the multi-biometric dataset increases the accuracy level for the ensemble systems.
Keywords: Ensemble systems; Cancellable Biometrics; Genetic Algorithms
Biometrics have been extensively used in diverse identity authentication applications [1-5]. These systems use human physical characteristics in order to guarantee the veracity of a claimed identity of a given user. Using biometric s avoids problems found in more traditional identification scenarios, such as the vulnerabilities of passwords and PIN-based systems. Biometric traits provide a number of desirable properties with respect to their use in an authentication system, such as reliability, convenience and universality, but their principal advantage is in binding data or activity unequivocally to an individual person. Thus, biometricbased authentication systems have stimulated an evolution in the verification and identification of individuals [6].
An important concern in biometric-based systems is related to the security of biometric data, mainly when a biometric template is compromised, perhaps because it is lost or stolen, or through unauthorized copies. It is important to emphasis that biometric information is permanently related to a specific user and cannot be changed in the event of template compromise. Therefore, a fundamental requirement to promote future deployment of biometric-based authentication systems is the development of techniques that allow the use of biometric data without compromising system security. Cancellable biometrics has been proposed to address these security issues, since they apply functions (generally not invertible) on the original biometric data in order to obtain transformed or intentionally-distorted representations [7]. It is the transformed representations which are used by the authentication system. In the case of data compromise, a biometric template can then be replaced through the application of a new transformation function [7].
An important way to increase security and performance (identification accuracy) in biometrics systems is to adopt a multibiometric approach. This fuses multiple sources of biometric information to combine identity evidence (discriminating information) in order to enhance classification performance [8]. Multi-biometric systems can be configured in different ways: for example, multi-sensor, multi-algorithm, multi-instance, multi-sample, and multi-modal systems [8]. In this paper we will focus on two configurations, the multi-algorithm (different transformation functions) and the multi-modal (different biometric modalities) approaches. Using a multi-biometric recognition system is expected to improve accuracy and help to defeat spoofing attacks. On the other hand, using cancellable biometrics aims to increase the security of biometric data. The combination of these two elements, however, aims to achieve a win-win scenario of security, performance and privacy. However, the combination of template protection methods and multi-biometrics has not been fully explored in the literature. There are some studies, such as those reported in [9-14], but most of these are based on cryptosystems methods.
In this paper, we propose the use of the multi-biometric approach with cancellable biometric data. In order to achieve efficiency in the proposed configuration, we apply an optimized ensemble system as the main fusion structure to combine the different information sources. In an ensemble system, each input pattern is handled in a parallel way by different classification modules (ensemble components), which separately produce their estimates of the class label [15]. These individual results are then fused by a combination module, which is responsible for producing the overall ensemble decision
In previous work, [14,16], we applied ensemble systems to cancellable biometrics and achieved very promising results, demonstrating that the use of ensemble systems improves the accuracy of cancellable biometrics. However, we noticed that some cancellable transformations can degrade the accuracy level of ensemble systems. Therefore, in order to increase the effectiveness of the ensemble systems, a genetic algorithm is applied in three separate parts of the design of an ensemble system for biometric recognition, aiming to maximize the performance of these systems. The first genetic algorithm is used in the cancellable transformation (preprocessing phase), and its goal is to improve the efficiency of the discretization process of the cancellable transformation through the use of optimized discrimination intervals. The second GA selects features for the individual classifiers of the ensembles and aims to add diversity to these systems. Finally, the third GA tries to improve the performance of ensemble systems through the use of an optimized set of weights that are used along with the output of the individual classifiers to define the final output of the ensemble systems (weighted combination methods).
Therefore, in this paper, we will show that we can improve even further the performance of cancellable multi-biometric processing through the use of more efficient ensemble systems. We also contribute to a better performance in terms of accuracy and reliability in the identification of the individual, an aspect of increasing importance as systems are more widely applied. Therefore, we can state that the main contributions of this paper can be described as follows:
1. Use cancellable transformations in multi-algorithm fusion of the chosen multi-biometric approach;
2. Apply two different biometric modalities, face and voice, either using the same cancellable transformation (multi-modal fusion) or using different cancellable transformations (multi-modal and multi-algorithm fusion);
3. Use ensemble systems as the fusion approach for the multi-biometric recognition;
4. Optimize the recognition process, using genetic algorithms in the preprocessing (adaptation of a cancellable transformation and feature selection) and in the structure of the ensemble systems (set of weights to be used in the combination module).
This paper is divided into nine sections and structured as follows. A review of related research is presented in Section 2. Multibiometric template protection methods are described in Section 3, while Section 4 presents a detailed explanation of cancellable biometric data, focusing on the cancellable transformations used in this paper. In Section 5, we describe the main concepts of ensemble systems and the genetic algorithms are described in Section 6. The experimental work is presented in Section 7, while Section 8 presents and discusses the experimental results. Finally, in Section 9, some final observations about this work are presented.
There are many studies reported in the literature which use genetic algorithms in the biometric-based recognition process (either using the original or cancellable data). These studies usually present efficient ways of dealing with the main problems involved in biometric-based authentication systems, such as in [17-24].
For original biometric data, it is described by Parsi et al. in [22] a new approach which applies a feature selection method using GAs. This work is based on facial recognition where GAs are used to select the most significant features of the dataset, which are subsequently classified by a k -NN (k -Nearest Neighbour) classifier in an adaptive system, called Training Swap. In the proposed technique, the alternative fitness function swaps the GA test and training data in each generation and the resulting fitness is evaluated. According to the authors, when using this approach, the GA does not converge quickly for a local minimum and the rate of final recognition is reinforced. The presented results show a significant improvement in performance, testifying to the efficiency of GAs when used in attribute selection. Still in the context of original biometric data, the use of GAs in multi-sample biometric recognition is proposed by Tan et al. in [23], using two sets of minutiae extracted from two different fingerprints. According to the authors, this technique aims to solve the problems found in low-quality images of fingerprints that present disorder or significant occlusions and clutter of minutiae features. The experimental results show that the proposed approach can achieve good performance, even when a great number of poor quality fingerprints are used as input to the system.
For cancellable biometric data, in Jeong, et al. [21], for instance, a genetic algorithm is applied in the pre-processing phase of a multi-sample biometric system. It uses features of face images extracted through two techniques: PCA (Principal Component Analysis) and ICA (Independent Component Analysis). Then, the image samples are normalized and transformed by a weight matrix that is determined by means of a genetic algorithm. This weight matrix is formed by an optimized weight vector that minimizes the error rate, providing an adjustment in the attributes of the original dataset through a fitness evaluation. According to the authors, this process results in a considerably improved system performance. In the sequence, the two datasets (normalized and transformed) are combined by the random addition of normalized and transformed attributes. This combination provides an improvement in the level of precision achieved and also generates a non-invertible transformed dataset.
Unlike most of this reported work, in this paper we propose to use genetic algorithms in three different situations, in which the first two are in the pre-processing phase, as in [21,22,24]. In addition, we apply a GA in the recognition structure (ensemble system) in order to obtain the most effective recognition structure to be used in the multi-biometric cancellable recognition.
There are many practical applications where the adoption of a single biometric modality is not able to meet all the required performance criteria. It is well known that the use of only one biometric modality tends to decrease the capability of biometricbased systems to have the needed requirements for an efficient system, in terms of performance (identification accuracy) and security (more difficult of being attacked). This problem may be more acute when working with cancellable data, where we have an increase in the complexity of the recognition process. Hence, solutions which involve the combination of different biometric sources (i.e. multi-biometric recognition) are of increasing interest. Multi-source fusion may occur in different phases of the recognition process: pre-processing (feature or sensor-level fusion), after the scores of the identification systems are produced (score-level) to the final phase, after a decision has been made (decision-level). In this paper, a score-level approach is considered, since this is the most natural choice when working with ensemble systems. Additionally, we can fuse the biometric data in several ways, such as:
• Multi-sensor: Only one biometric modality is used and the combination is made using different sources (sensors);
• Multi-algorithm: Only one biometric modality is used and we apply different recognition methods;
• Multi-sample: Only one biometric modality is used and we apply different pre-processing methods (feature extractors, different fingers or eye) of this biometric modality;
• Multi-modal: The combination of more than one biometric modality.
In this paper, we combine biometric data using multi-algorithm and multi-modal fusion approaches. The multi-biometric approach can be applied to either the original or the cancellable biometric data, and a number of attempts have been made to combine multibiometric recognition with cancellable biometrics, such as in [9-13]. However, most of these studies are based on cryptosystems template protection and using feature-level fusion.
The fact that biometric traits are unique and are permanently related to a user makes the security of biometric systems an important issue, since it is impossible to achieve its substitution or cancellation in the case of data compromise. This is one of the biggest problems in biometric-based systems. One of the solutions to this problem is the storage of a protected biometric model instead of the original biometric sample. In doing this, we eliminate any possibility of leakage of the original biometric trait [25]. In the literature, we can find many biometric template protection methods that, according to Jain et al. [7], can be divided into two types, which are: Biometric cryptosystems (some public information about the biometric templates is stored and a cryptographybased procedure is applied) and Feature transformations, or simply cancellable trans- formations, (a transformation function (f) is applied to the biometric template (T) and only the transformed template (f(T)) is stored in the dataset).
According to the characteristics of the transformation function f, the feature transformation can be further divided into two classes: salting and non- invertible transformations. In the salting approach, the used transformation function f is invertible and, therefore, its security is based on a secret key or password [26]. Thus, if an intruder obtains access to the security key, the biometric data will be at risk. On the other hand, non-invertible transformations use one-way functions, making it computationally difficult or impossible to achieve an inversion of the transformed model, even having access to the security key. In our work reported here, we will focus on the use of non-invertible transformation functions. Hence, in the remainder of the present article, the terms transformation function or cancellable transformation will be taken as referring to the non-invertible case. We will use three cancellable transformations that will be presented in the next three subsections.
Biohashing uses a cancellable transformation that transforms the original biometric samples into a non-invertible number [27]. This technique has originally been used with biometric modalities such as fingerprint [27]. In this paper, we have applied this cancellable transformation to the face and voice biometric modalities. The original Biohashing procedure can be described as follows.
1. With the original biometric model Γ Є Rn, with n being the number of attributes of Γ, a set of pseudo-random vectors {pi ЄRn | i = 1, ..., m} is generated, where m is the number of vectors of dimension n and m ≤ n;
2. The Gram-Schmidt algorithm is then applied in {pi ЄRn | i = 1, ..., m} to obtain m orthonormal vectors {oi Є Rn | i = 1, ..., m};
3. The inner product between the original biometric vector Γ and each pseudo- random orthonormal vector oi is calculated, {(Γ | oi) | i = 1, ..., m}, where (o | o) indicates the inner product operation.
4. Finally, a binary discretization of the values obtained in the inner products is performed and we obtain an m-bit Biohashing
model, {b = bi | i = 1, ..., m}, where: with τ being an empirically determined threshold.
In this paper, we use an adaptation of this model, which was originally proposed by Pintro in [28]. This adaptation modifies step 4 of the standard Biohashing procedure (discretization function). It consists of two basic steps, which are: discretization of data into 4 values [0;0.33;0.66;1], instead of only 2 values [0;1], and the use of GAs to determine which are the optimal intervals for discretization. The purpose of using more discretization values is to enlarge the space of coding, enabling a better representation of the transformed dataset, without losing the characteristics of the Biohashing function. An initial investigation has led us to select 4 as the number of possible values for the discretization. Therefore the proposed discretization step is implemented as follows. First, a standard normalization is carried out on the result of step 3. Then, the normalized data is discretized according to the following intervals:
The values for the discretization coefficients a, b and c of Eq. 2 are deter- mined by a genetic algorithm. The most important parameter in the Biohashing function is m, which represents the number of pseudo-random orthonormal vectors. This value must be determined empirically and corresponds to the number of attributes for each instance of the transformed dataset.
This function generates a new biometric model based on the extraction of points of an interpolation process which is applied in the attributes of the original biometric model. The use of an interpolation-based method for obtaining cancellable biometric data was originally proposed by Pintro in [28] and, in this work, we adapt its use for face and voice modalities. It is a simple method and it adds the security level of a biometric system, since an inversion of the trans- formed function is difficult to achieve. This method then satisfies two main requirements for a cancellable transformation, efficiency and simplicity. The interpolation process is described as follows.
1. For each sample of the original biometric model Γ Є Rn, where n is the number of attributes of Γ, the interpolation polynomial of the attributes of the biometric model is applied to obtain a function f(x). Therefore, we have a function f(x) for each biometric sample of the dataset. It is important to use a polynomial function with a significant degree g, usually given by the highest degree supported by the computational system, in order to have good approximation functions of the discretized data;
2. A vector of random numbers is generated δ Є Rd for all users. It consists of uniformly distributed pseudo random numbers, where d is the dimension of δ. The value of d is empirically defined and can have an impact on the behaviour of the model (usually d = n);
3. We then apply individually all created interpolation functions f(x) to the vector δ, generating the output the transformed dataset.
In the cases where the current random vector is corrupted or stolen, a new random vector can be used and we obtain a different transformed vector. Also, the interpolation model depends on variables such as the size d (step 2) of the random vector and the degree of the polynomial interpolator g.
The BioConvolving function applies linear combinations of sub-parts of the original biometric template to create the protected template. The original biometric sequences are divided into W non-overlapping segments, based on a randomly selected transformation key d. Then, the transformed functions are obtained by performing a linear convolution between the resulting segments. This approach was originally proposed for use with a handwritten signature biometric [29] but here we apply it to face and voice data. A general description of BioConvolving is presented as follows.
1. Define the number of segments to divide the original biometric model (W).
2. Select randomly a number (W − 1) of values dj. The selected numbers have to be an integer between 1 and 99. In addition, these
numbers must be ranked in an increasing order. The selected values are arranged in a vector d = [d0 , ..., dW ], having kept d0 = 0
and dW = 100. The vector d represents the key of the adopted transformation.
3. Convert the values dj into bj based on the following function bj = round((dj/100)*n), j = 0, ..., W, where n is the number of attributes
and round represents the nearest integer,
4. Divide the original sequence Γ Є Rn , into W segments Γ(q) of length Nq = bq − bq−1 and which lies in the interval [bq−1 , bq] of the attributes;
5. Apply the linear convolution of the functions f(Γ(q)), q = 1..W to obtain the transformed function
f = Γ(1) ✳ ... ✳Γ(W) (3)
A transformed function is thus obtained through the linear convolutions of parts of the corresponding original functions Γ. Due to the convolution operation in step 3, the length of the transformed functions is equal to K = n−W+1, being therefore almost the same as the original data. Final signal normalization is then applied, oriented to obtain zero mean and unit standard deviation transformed functions. Different transformed results can be obtained from the same original functions, simply varying the size or the values of the parameter key d.
As already noted, a natural way to combine different biometric sources is through the fusion of experts, an approach producing what are generally referred to as multi-classifier systems or ensemble systems [15]. Figure 1 illustrates the general structure of an ensemble system, which is composed of a set of c individual classifiers (ICs) which are organized in a parallel configuration. Therefore, unlabelled patterns {xi Є Rd |i = 1, 2, ..., n} are presented to all individual classifiers in a parallel way and a combination method combines their output to produce the overall output of the system O = C omb(yj ), {yj = (yj1 , ..., yjk |j = 1, ..., c and k = 1, ..., l}, where the number of individual classifiers is defined by c and l describes the number of labels in a dataset (Figure 1).
For ensemble systems, individual classifiers must offer complementary information about an input pattern and this complementary information tends to increase the effectiveness of the whole recognition process [15,30]. There- fore, it is important, when designing ensembles, to consider carefully individual components (classifiers) of an ensemble and its combination technique. With regard to the first of these, the ensemble size (number of individual classifiers) and composition (classification algorithms that comprise the ensemble systems) must be defined.
The design of an ensemble system can adopt of one two principal broad structures, designated respectively, heterogeneous or homogeneous structures. Different classification algorithms are selected as individual classifiers in the first case and only one classification algorithm is selected in the second case (for instance, ensembles of decision trees). When choosing the individual classifiers of an ensemble, the ensemble components must be different from each other, so that different, but complementary, information is generated, thereby improving the performance of the overall system. This characteristic is called ensemble diversity. Diversity in ensemble systems can be achieved when the individual classifiers are implemented under different circumstances, such as: parameter setting, classification type and datasets. In our empirical analysis, we use different classification types (heterogeneous structures) and datasets. In the case of different datasets, we apply feature selection methods which usually increases the diversity of the members of an ensemble.
Once the set of individual classifiers is created, an effective way of combining their estimates of the class label must be determined. Based on their functioning, one of the following three strategies is typically adopted: 1) Fusion: the combination module takes into consideration all the individual classifiers when defining the final output of the ensemble; 2) Selection: one individual classifier is selected and is used as a guide to provide the output of the system; and 3) Hybrid: we select from the strategies cited above. Basically, the idea is to use selection if and only if the best classifier is particularly effective in classifying the test pattern. Otherwise, fusion is used.
In this paper, we use four fusion-based combination methods in the ensemble systems, which are: Majority vote, sum, support vector machine (SVM) and k-nearest neighbor (k-NN) algorithms. We use traditional classification algorithms as the combination model, in which the combiner receives real numbers as input and provides the class label as output.
In this paper, we analyse the benefits of using an optimized recognition structure for cancellable multi-biometric recognition. In order to do this, an empirical analysis is conducted. In this paper, we decided to use two biometric modalities, Face and Voice. The main reason for this choice is that these two modalities are the ones which have offered a high number of studies in the literature, such as in [31-34].
The general methodology of the empirical analysis is illustrated in Figure 2. In this methodology, we present a biometric template X = x1, x2, ..., xn where n represents the number of attributes of a biometric modality. This biometric template passes through three cancellable transformation modules (Biohashing, Interpolation and BioConvolving), producing three transformed datasets for each biometric modality (TF for face and TV for voice). It is important to observe that the Biohashing function uses a genetic algorithm to provide the best intervals for the discretization process. The transformed datasets are passed by a genetic algorithm for feature selection and they are then trained by individual classifiers. A genetic algorithm is then applied to define the best set of weights for the fusion approaches.
In this methodology, we apply a decision-level fusion approach that uses one of the four possible approaches (uni-modal and unialgorithm; uni-modal and multi-algorithm; multi-modal and uni-algorithm; and multi-modal and multi- algorithm). In the first approach, uni-modal and uni-algorithm, only information from one cancellable transformation of one specific biometric modality is taken into consideration. If we add one or more cancellable transformations, then we have the second approach, uni-modal and multi-algorithm. If we maintain one cancellable transformation and add one or more biometric modalities, we have the third approach, multi-modal and uni-algorithm. Finally, if we add one or more cancellable transformations and one or more biometric modalities, we have the last approach, multi-modal and multi-algorithm. Here, we will analyse all these four fusion approaches.
For convenience and clarity, Figure 2 shows only one possible combination (illustrated by means of the arrows linking individual classifiers and fusion modules), but in practice all the cancellable transformations are combined (Figure 2). Similarly, we present only the multi-biometric cancellable scenarios. However, for comparison purposes, the datasets with the original templates (original dataset) are considered in the empirical investigation and the genetic algorithm will also be applied to the original dataset.
The basic operating principle of genetic algorithms is to treat the possible solutions of a problem as individuals of a population, which will develop at each iteration or generation. In the context of ensemble systems, GAs has been widely used to optimize the structure of ensembles, including the features used by the individual classifiers. In this paper, we use GAs to improve the performance of the recognition process for cancellable multi-biometric systems. In order to do this, three genetic algorithms are used. The first is applied in the Biohashing method, the second to select features for the individual classifiers of the ensemble system and the third to define the optimal set of weights for the combination module of an ensemble system.
First, we apply a standard genetic algorithm to define the best intervals for discretization in the Biohashing cancellable transformation. The chromosomes are represented by a vector of real numbers that lie in the [0,1] interval and contain 3 values (one value for each coefficient of Equation 2). The initial population is randomly chosen. The population size is empirically defined as 250. In this case, we selected ten population sizes and we run the genetic algorithms using these sizes in a validation set. Then, the population size that obtained the best performance for both datasets over the validation set was selected. Finally, standard genetic operators (mutation and crossover) are used.
The second genetic algorithm is used to select attributes of the individual classifiers of an ensemble system. In this case, a binary chromosome is used to represent a possible solution. The size of the chromosome is C ✳ N, where C represents the number of classifiers of the ensemble and N represents the number of attributes of the dataset. In this chromosome, the first N bits represent the feature subset for classifier C1, followed by the N bits for classifier C2, and so on. In each classifier, these bits represent the absence (0) or presence (1) of the corresponding attributes in the feature subset of the classifier. The initial population is formed by M individuals, with M = 250 for the experiments reported here. For the genetic operators, a standard one-point crossover and bit flipping mutation are used.
The choice of a fitness function is a problem when using an optimization technique in ensemble systems, since we can choose from filter-based approaches (independent of the learning algorithm) or wrapper-based approaches (a learning algorithm is used to guide the whole search). The filter-based approaches tend to have more flexibility, but with the drawback of low accuracy. The wrapper-based approaches are more accurate, but usually require a complex and time consuming process [35,36]. In this paper, for the first two genetic algorithms, we use a simplified wrapper-based approach in which we have chosen the average accuracy of two different learning algorithms (Naive Bayesian and k -NN) as the fitness function. The choice of these learning algorithms is because they are well-known simple methods, in terms of time consuming processing, and they have different classification criteria in their decision-making. This allows the fitness function to assess the possible solutions from two different points of view, increasing the ability to generalize.
For the third genetic algorithm, a set of optimal weights is defined. In ensemble systems, weights are associated with every example to denote the confidence (influence) of the individual classifiers in classifying the input pattern to a particular class. For this GA, we use a population of size 200, with each individual being represented by a vector of real numbers (in the [0,1] interval), representing the weights for each class of each individual classifier. The population is initialized assigning 1 to all weights of all individual classifiers. We then apply mutation and crossover as genetic operators and the stopping criterion is defined by the maximum number of iterations (varying from 400 and 1000, depending on the dataset used). Once again, we used a validation set to evaluate the performance of the genetic algorithms with different number of interactions. Then, for each dataset we selected the number of interaction that provided the best performance. As the fitness function, we use the accuracy level of the ensemble systems. Unlike the first two genetic algorithms, this GA is applied at the end of the recognition process and we can train all individual classifiers in advance since the possible solutions use the same trained individual classifiers. In this case, we can use the accuracy of the whole ensemble without incurring significant time overheads.
As we use an initial population composed of identical chromosomes (vectors of 1's), we apply the mutation operator with a variable rate. For the first iteration, the mutation rate is 20% and a reduction of 1% is applied every five iterations until it reaches 1% and it stabilizes. In addition, we apply the crossover operator only after the third iteration.
In this investigation, we use three classification algorithms as individual classifiers, which are: k-NN (Nearest Neighbour), Naive Bayes and Multi-layer Perceptron Neural Networks (MLP). We selected these classification algorithms because they provide diversity in their classification criteria. In addition, in the decision-making process, the decisions of individual classifiers are combined by fusion-based functions to provide the final output of the ensemble systems. In this analysis, we use four methods, which are: Sum, majority voting, k-NN and SVM (Support Vector Machine). In addition, k-NN and SVM are considered trainable combination methods. In these cases, we generate a validation dataset for training these methods. All classification and optimization methods used in this study are coded in Matlab.
Three ensemble sizes are investigated here, with c = 3, 6 and 12 individual components. Additionally, we investigate several configurations for each ensemble size, including homogeneous and heterogeneous ones. As we aim to present the overall performance achieved by the ensemble systems, however, the values presented in this empirical analysis describe the accuracy averaged for all possible structures of the ensemble systems.
A standard k-fold cross validation method, with k = 7, was used in order to evaluate the classification systems. In order to compare the accuracy of the classification systems, the Wilcoxon signed-ranks test is used to evaluate the accuracy levels produced by the ensemble systems. We selected this test because it is a non-parametric test which is applied in order to compare two samples (related, matched or repeated measurements of a single sample) to evaluate the difference of their population mean rankings, whether statistically significant or not. This test can be used as an alternative to the student's t-test in cases where a population cannot be seen as normally distributed [37]. This test uses a degree of freedom (ρ), where ρ = 0.05 is used in this study.
Finally, for the multi-modal fusion approaches, we combined two biometric modalities (face and voice). In this combination, we performed two analyses. In the first, two thirds (2/3) of the individual classifiers use as input the face dataset and one third (1/3) used voice and, in the second analysis, the opposite proportions are chosen.
The datasets used in our empirical investigation were the TIMIT dataset [38] for voice and The AR Face Database [39] for Face. The original and transformed datasets were composed of 100 different classes, with 7 instances per class, making a total of 700 instances for each dataset.
The voice dataset used in this investigation is extracted from the TIMIT database [38]. The procedure used to generate the original voice data used in this analysis consists of three main steps, which are: 1) Pre-processing: This step includes actions such as preemphasis, segmentation of data (frames), removal of silence and windowing of the voice data; 2) MFCC: In this step, MFCC (mel-cepstral coefficients) are extracted from each window (20ms duration extracted at a rate of 10 ms) of the signal [40]. In our work, we extract 12 coefficients; and 3) GMM-UBM: In using MFCC, we encounter input with variable size based on the length of the sample. Then, we apply the generative GMM-UBM (Gaussian Mixture model - Universal Background model) model in order to create feature vectors of fixed size to be used by any classification method. This procedure is similar to the one proposed by Kinnunen et al. [41]. Therefore, the attributes of the original voice dataset represent the mixtures of the Gaussian model provided by a GMM-UBM model. In this work, we use 30 mixtures and 12 MFCC coefficients, making a total of 360 attributes.
For the face images, features are extracted by the ICA method (independent component analysis) [42], which is a method for separating a multivariate signal into additive subcomponents by assuming that the subcomponents are non- Gaussian signals and that they are all statistically independent of each other. In this investigation, we use the 100 most relevant values for composing the original dataset. Therefore, the face dataset is composed of 100 attributes.
For the Biohashing dataset, we apply the procedure described in 4.1 and use a value of m equal to the number of attributes of the original datasets. In this case, the Biohashing datasets are composed of 360 and 100 attributes for voice and face, respectively.
In the interpolation process, Section 4.2, the highest degree of the polynomial interpolation allowed by the system was 6. Because of this, the original biometric traits are very large and a polynomial of degree 6 is not able to create a function of acceptable interpolation. Therefore, the original biometric samples are divided into I separate parts, with I = 10. The random vectors are also divided into I intervals (with 36 attributes for the random vector of voice and 20 attributes for face). Subsequently, for each subset of a biometric sample, an interpolation function is generated. After this, the transformed models M are created connecting the results of the interpolation function in all I intervals, making a total of 360 attributes for voice and 100 attributes for face.
In the BioConvolving function, we transform the biometric models into matrices, and these matrices, of 30 lines by 12 columns for voice and 10 lines by 10 columns for face, where each column is treated as a time sequence. The time sequences are divided into 2, W = 2, intervals, making the number of attributes equal to the original dataset, 360 for voice and 100 for face.
In this paper, we will only analyse the performance of the cancellable biometric system. Although there are two more important criteria for cancellable biometric, diversity and non-invertibility, as we are not proposing new trans- formation functions, we will only analyse the effect, in terms of performance, of these transformation functions when using ensemble systems and applying ensemble systems. These two criteria were investigated in the original paper of the transformation functions.
Additionally, it is important to emphasize that we have addressed in this paper a user biometric-based identification task. Therefore, when a biometric sample is provided, the classification systems output a class label which corresponds to a specific individual user. Alternatively, we could have implemented a verification task, as in [43-45]. However, identification is a U-class problem (where U is the number of enrolled users) and verification is, in effect, a two-class classification problem. In this case, from a classification point of view, identification is the more complex and time consuming task. In addition, as we want to analyse the benefits of wellestablished classification structures, we have chosen to focus on identification. Nonetheless, the proposed methodology can be easily adapted for verification tasks.
Aiming to demonstrate the benefits that genetic algorithms can bring to the development of more accurate biometric systems, this section presents the experimental results individually for all three genetic algorithms that are used. The first genetic algorithm is applied in the Biohashing function and the results are illustrated in Table 1, which shows the average accuracy of the individual classifiers when using the standard Biohashing and the adapted model proposed in this paper. These values represent the averaged results of all individual classifiers obtained in this experimental analysis. In addition, as we wish to observe the direct effect of the transformation functions, we considered only the individual classifiers.
In analysing Table 1, we can observe a substantial improvement in accuracy presented by the adapted model, reaching 5% points for voice dataset. Applying the statistical test shows that the improvements achieved with the adapted Biohashing are statistically significant in both cases. The use of the adapted Biohashing method helps to improve the accuracy of cancellable biometric systems. Therefore, henceforth, the Biohashing function used in this experimental work is the adapted one.
Table 2 presents the results of using GA to select features for the individual classifiers of an ensemble system, for the original datasets and all three transformed datasets (BioConvolving, Interpolation and Biohashing) using both biometric modalities. Once again, as the feature selection process has a direct impact in the accuracy of the individual classifiers, this table presents the results obtained by the individual classifiers. The NumAtt column represents the number of attributes of the corresponding dataset.
As can be observed from Table 2, the use of genetic algorithms causes a significant reduction in the number of attributes (around 38% for the face dataset and 56% for voice). However, the accuracy of the individual classifiers using feature selection was slightly higher than the datasets without feature selection (complete dataset), for all analysed cases. We then apply the statistical test, on a two-by-two basis, to evaluate whether the observed improvement is statistically significant and this proved not to be statistically significant in any case. Nevertheless, it is important to emphasize that the reduced datasets decrease drastically the problem dimensionality (number of attributes) and offered a similar accuracy, when compared with the complete datasets. Therefore, hereafter, we will use the reduced datasets (with feature selection) in our analysis.
Next we will analyze the use of GAs in determining the set of weights to be used in the combination functions, and this result is shown in Table 3. This table reports the performance of the ensemble systems both with a uniform set of weights for all classifiers (standard ES) and when a GA has been applied to determine this set of weights (ES+GA). In this table, we illustrate the results of the ensemble systems for both biometric individually (face and voice) and for the combination of them (Face+voice). The shaded cells in Table 3 represent the highest accuracy achieved, for the ES and GA+ES cases, and for each dataset. In addition, the underlined numbers represent the cases where the improvement is statistically significant.
Table 3 shows that generally the use of GAs in determining the set of weights is an important tool in the development of more accurate ensemble systems, since it generates a significant increase in the accuracy achieved in all analysed cases. Also, by applying the statistical test, we can observe that the differences in accuracy delivered by the ES+GA ensemble systems are statistically significant for four combination methods (in voice, face and face+voice), rejecting the null hypothesis of equivalence. The only exception is when using SVM- based combination in which ES+GA ensemble provided higher accuracy than standard ensembles, but only marginally. We believe that the application of the GA improved the discriminability of the problem, decreasing the difficulty level of the classification process. Therefore, simple combination methods in the ensemble systems, such as the Sum and Voting approaches are then sufficient. Therefore, the difference in accuracy when moving from standard to ES+GA is high only for these simple combination methods.
In summary, we can observe that the genetic algorithm is an adaptable optimization technique since it can have positive effects on the performance of biometric systems when using at different stages of the recognition process.
This section reports the results of applying transformation functions (individually or combined), analysing the benefits of the different cancellable trans- formations when applied to the optimized ensemble systems. Tables 4 and 5 present the results obtained, individually and combined. These tables show the accuracy achieved and the standard deviation of the classification systems (individual classifiers-Ind, and ensemble systems combined with Sum, Majority Voting-VT, Naive Bayes-NB, k-NN and SVM). The results were obtained with homogeneous and heterogeneous structures, using 3, 6 and 12 individual classifiers. In order to provide a general perspective on the obtained results, the values presented in this section describe the accuracy averaged by all possible structures of the ensemble systems.
The shaded cells indicate the best results (the highest accuracy level for each line) attained by an ensemble system of the corresponding dataset, either original or transformed.
Individual Transformation Functions: Here, all individual classifiers of an ensemble system are trained individually for one cancellable transformation, either using one biometric modality (uni- algorithm uni-modal fusion) or combined datasets (unialgorithm multi-modal fusion). Table 4 presents the results of the classification systems for the biometric modalities Voice and Face individually, as well as the combined scenario.
The results in Table 4 illustrate, as expected, that the approach using a single cancellable transformation is not sufficient to provide an improvement in accuracy level of the ensemble systems. From these results, it can be seen that the use of cancellable transformation functions decreases the accuracy level achieved with the voice and face data in most of the analysed cases. In some cases, for the voice dataset, the use of cancellable transformation functions caused an improvement in the accuracy of the ensemble systems. Nevertheless, these improvements were not proved to be statistically significant. These results illustrate the need for approaches that involve more elaborate transformation functions in order to overcome the increase in complexity of the cancellable data.
In order to evaluate whether the improvement reached by the transformed datasets is statistically significant, we applied a statistical test (Wilcoxon signed-ranks test) comparing the best result (highest accuracy rate) with the second best result (second highest accuracy rate). In cases where the best result was a transformed dataset (except the original column), the statistical test always compared the best result with the original dataset. The statistically significant values are underlined. As a result of the statistical test, we can observe that the use of the transformed data cause a statistically significant decrease in only one case (voice dataset with ensembles combined by NB). This means that although there is a decrease in the accuracy, at least one cancellable transformation pro- vided accuracy rates similar to those delivered by the original dataset in most cases. On the other hand, the use of the transformed data causes a statistically significant increase in two cases (Biohashing for voice dataset with ensembles combined by Sum and MV). In general, from a statistical point of view, the original dataset and the best cancellable transformation generate a similar accuracy rate.
Among the individual cancellable transformations, the interpolation function provides the highest accuracy for Face, while the Biohashing function achieves the highest accuracy level for voice and combined scenarios. This result shows that there are some differences in the different datasets and this may make a cancellable transformation viable for one specific application but not for another.
In analysing the effect of using a multi-biometric configuration (uni-algorithm multi-modal fusion), in comparison with the individual biometric modalities, we can see that in relation to the accuracy of the multi-biometric (combined) dataset, they provide the highest accuracy when analysing the ensemble systems. These results show that the use of ensemble systems applied to the multi- biometric dataset, along with ways to improve its effectiveness, have overcome the problems found in the individual modalities and have provided the highest accuracies achieved in this investigation.
In this section, the results of the combination of the cancellable transformations are presented. As we have three cancellable transformations, the combination was investigated on a two-by-two basis (ConvBio for Convolution and Biohashing; ConvInt for Convolution and Interpolation; and BioInt for Biohashing and Interpolation) and the combination of all three functions (All three columns). Table 5 reports the accuracy and standard deviation of the classification systems in this combined scenario. For comparison purposes, the results of the ensemble systems using the original datasets are also provided in this table. Once again, the underlined numbers represent the highest accuracy level achieved for the ensemble systems, for each dataset.
Here, two different analyses are considered. The first compares the results of the ensemble systems with and without cancellable transformations. We see that the use of more than one cancellable transformation causes an improvement in the accuracy level in almost all cases. When combining all three cancellable transformations, for instance, this results in an improvement in all cases (ensemble systems), when compared with the original dataset.
We apply the same statistical test as used in the previous section, comparing the original dataset with the best transformed dataset (All Three dataset for all cases). The statistical test shows that the use of the transformed data causes no statistically significant decrease in performance. On the other hand, the use of the transformed data causes a statistically significant increase in almost all cases (14 out of 15 ensemble scenarios). In general, from a statistical point of view, the combination of all three cancellable transformations causes an increase in the accuracy rate of the ensemble systems.
In analyzing the use of more than one cancellable transformation, in comparison with one cancellable transformation, this brings about an improvement in the achievable accuracy in almost all cases. Once again, we emphasize the performance when combining all three cancellable transformations, which causes statistically significant improvements in all cases for the ensemble systems. The only exception is for ConvInt, which did not cause an improvement in accuracy.
Once we have carried out an investigation of the genetic algorithms and the cancellable data, we investigate the impact of a combination approach in the context of ensemble systems. From a general perspective, of the combination methods, the highest accuracy is achieved using the Sum method for most of the analyzed cases. However, in some cases, ensembles combined using SVM delivers the highest accuracy levels. Therefore, we can state that there is no "best" combination method from a general perspective. However, we can analyze the impact that the choice of combination method can have on the accuracy of the different ensemble structures over the different fusion approaches. In order to do this, Figure 3 shows the accuracy achieved by ensembles combined by the Sum and the SVM methods, when varying the main parameters of an ensemble composition (ensemble structure and number of individual classifiers).
As can be observed from Figure 3, for the first fusion approach (uni-modal and uni-algorithm fusion), ensembles combined by the Sum method show the highest accuracy for the face dataset and ensembles combined by means of the SVM method produce the highest accuracy for the voice dataset. For the other fusion approaches, as the level of diversity increases (more than one dataset for the individual classifiers), we begin to observe a superiority, in terms of accuracy, of ensembles combined by the Sum method. For instance, when using three cancellable transformations in the second fusion approach (right graphic of the second line), we achieve the highest diversity level of this fusion approach and ensembles combined by Sum show the highest accuracy in 11 cases (out of 12), even in the voice dataset. The same scenario also happens in the fourth fusion approach with three cancellable transformations, in which ensembles combined by Sum show the highest accuracy in all 6 cases. These results show that when we have a low diversity level, we should use more elaborate and powerful combination modules in order to overcome the lack of diversity. In contrast, when the level of diversity increases, simple combination methods such as Sum, can be used with more satisfactory results (Figure 3).
In analyzing ensemble systems when varying the number of individual classifiers, performance usually increases when we increase the number of individual classifiers. However, this behavior is not observed very often when increasing the level of diversity of the ensemble systems, since the accuracy levels tend to stabilize or even decrease when increasing the number of individual classifiers. In relation to ensemble structures, the accuracy is usually higher for the heterogeneous structures than for the homogeneous structures. Once again, ensembles combined by SVM usually generate the highest accuracy levels in the homogeneous structures (low diversity level) while ensembles combined by Sum produce the highest accuracy levels in the heterogeneous structures (high diversity level).
This work has presented a new approach for the identification of multi- biometric cancellable identification, where genetic algorithms are applied in three different stages of the recognition process (cancellable transformation, feature selection and determination of the set of weights for the combination module) and ensemble systems are used as the recognition structure. We have used as examples two different biometric modalities (face and voice) separately and in a multi-modal context.
Through this analysis, an important conclusion which can be drawn is that the use of GAs in the search for more efficient and secure biometric systems has had a positive effect, since this increases the accuracy level of the ensemble systems in all three applications. In addition, this shows the flexibility of genetic algorithms, since their application is possible in different parts of a biometric recognition system, whether it is to optimize the set of weights in an ensemble system or to refine the processing of a cancellable transformation or even selecting features for the individual classifiers. Our approach means that we can implement a secure system while, at the same time, maintaining the highest accuracy level.
Another observation emerging from our work is that the combination of different cancellable transformation functions is more efficient than using individual transformation functions. We believe that this combination scenario compensates for the loss in performance attributable to the increased complexity associated with the individual transformation functions. The use of multi-modal fusion does cause an increase in the accuracy achievable by ensemble systems only when using one cancellable transformation. In this case, the diversity created by the use of two biometric modalities enhances the performance of the ensemble systems.
In general, we can conclude that the results of this study are very promising, showing numerous tools that can help the development of more efficient biometric systems, something increasingly important in today's society. The use of other cancellable transformations functions, as well as their application to other biometric modalities is the subject of ongoing research. Nevertheless, it is expected that this preliminary study can be beneficial to the development of biometric systems which are more generally viable in many current applications.
 |
| Figure 1: The general structure of an ensemble system |
 |
| Figure 2: The general structure of the proposed methodology |
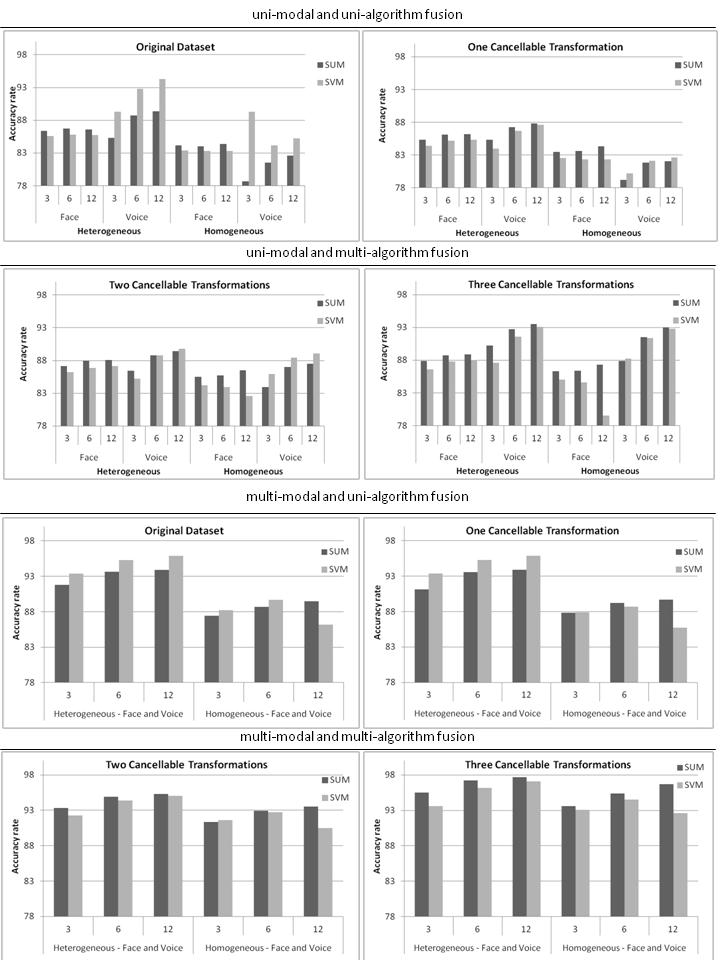 |
| Figure 3: Accuracy rate of the ensemble systems combined with Sum and SVM for all four fusion approaches, varying the number of individual classifiers (3, 6 and 12) and ensemble structures (homogeneous and heterogeneous) |
| FACE | VOICE | ||
|---|---|---|---|
| Standard | Adapted | Standard | Adapted |
| 76.24±4.24 | 78.37±4.69 | 75.53±5.66 | 80.5 ±2.77 |
| Table 1: Accuracy level (%) and standard deviation of the individual classifiers with the standard and adapted Biohashing | |||
| Datasets | FACE | |||
|---|---|---|---|---|
| Traditional | Feature Selection | |||
| NumAtt | Accuracy | NumAtt | Accuracy | |
| Original | 100 | 79.23±5.67 | 57 | 79.38±4.10 |
| BioConvolving | 100 | 79.07±4.65 | 55 | 79.12±3.65 |
| Interpolation | 100 | 78.65±5.03 | 61 | 78.75±4.00 |
| Biohashing | 100 | 78.12±5.64 | 74 | 78.37±4.69 |
| VOICE | ||||
| Traditional | Feature Selection | |||
| Datasets | NumAtt | Accuracy | NumAtt | Accuracy |
| Original | 360 | 78.01±6.84 | 144 | 78.09±10.49 |
| BioConvolving | 360 | 78.27±5.12 | 168 | 79.45±3.62 |
| Interpolation | 360 | 75.17±5.10 | 173 | 75.96±8.32 |
| Biohashing | 360 | 79.68±4.23 | 47 | 80.50±2.77 |
| Table 2: Accuracy level (%) when selecting features for the individual classifiers | ||||
| FACE | VOICE | FACE+VOICE | ||||
|---|---|---|---|---|---|---|
| ES | ES+GA | ES | ES+GA | ES | ES+GA | |
| Sum | 84.29±5.29 | 90.38±4.96 | 87.02±5.38 | 93.89±4.98 | 94.25±3.64 | 96.86±2.15 |
| MV | 82.13±4.58 | 87.34±4.35 | 84.63±5.96 | 90.77±5.74 | 87.90±5.02 | 93.35±2.76 |
| NB | 81.66±4.55 | 86.15±3.87 | 81.3±40.88 | 86.94±4.09 | 86.18±6.73 | 90.67±3.92 |
| k-NN | 83.07±4.04 | 87.80±4.23 | 86.13±4.97 | 91.19±4.36 | 92.07±3.92 | 95.13±2.08 |
| SVM | 86.94±4.36 | 87.32±4.54 | 89.3±5.00 | 89.7±5.26 | 94.38±2.72 | 94.67±2.9 |
| Table 3: Accuracy level (%) and standard deviation for the ensemble systems without and with a genetic algorithm to define the set of weights | ||||||
| FACE | ||||
|---|---|---|---|---|
| Original | BioConvolving | Interpolation | Biohashing | |
| Ind | 79.17±4.35 | 78.85 ±3.92 | 78.57 ±4.23 | 78.15 ±4.89 |
| Sum | 85.38 ±3.89 | 84.83 ±3.62 | 84.67 ±3.79 | 85.42 ±4.73 |
| MV | 84.23 ±5.00 | 83.95 ±4.61 | 83.82 ±4.63 | 84.33 ±5.72 |
| NB | 79.98 ±5.37 | 79.15 ±5.09 | 79.08 ±5.69 | 79.65 ±6.38 |
| k-NN | 82.33 ±5.09 | 81.52 ±4.88 | 81.35 ±4.86 | 81.82 ±6.05 |
| SVM | 83.18 ±5.76 | 82.05 ±6.03 | 82.87 ±4.56 | 83.085.63 |
| VOICE | ||||
| Original | BioConvolving | Interpolation | Biohashing | |
| Ind | 77.98 ±6.7 | 77.52 ±3.46 | 76.00 ±8.41 | 77.62 ±2.75 |
| Sum | 84.37 ±3.80 | 84.43 ±3.41 | 82.17 ±8.19 | 87.88 ±4.28 |
| MV | 84.43 ±3.68 | 84.03 ±3.40 | 82.10 ±7.55 | 87.60 ±3.27 |
| NB | 83.40 ±4.07 | 76.08 ±3.40 | 76.63 ±4.34 | 75.47 ±5.82 |
| k-NN | 84.70 ±3.39 | 80.85 ±3.76 | 79.72 ±8.59 | 84.77 ±4.19 |
| SVM | 87.83 ±3.09 | 83.00 ±3.79 | 83.05 ±8.22 | 86.98 ±3.04 |
| FACE+VOICE | ||||
| Original | BioConvolving | Interpolation | Biohashing | |
| Ind | 79.12±4.51 | 78.87 ±6.01 | 77.97 ±6.27 | 78.67 ±3.75 |
| Sum | 90.82 ±3.13 | 90.90 ±5.31 | 90.62 ±5.70 | 90.32 ±5.16 |
| MV | 90.28 ±3.63 | 90.30 ±5.75 | 90.17 ±5.80 | 89.67 ±5.11 |
| NB | 87.63 ±4.47 | 83.92 ±6.40 | 85.05 ±7.24 | 81.4 ±9.05 |
| k-NN | 89.45 ±3.99 | 87.48 ±6.12 | 87.72 ±6.37 | 87.1 ±5.72 |
| SVM | 91.45 ±3.79 | 88.83 ±6.43 | 90.15 ±5.88 | 88.88 ±4.66 |
| Table 4: Accuracy level (%) and standard deviation of the classification systems when using the unialgorithm uni-modal fusion (Face and Voice) and the uni-algorithm multi-modal fusion (Face+Voice) | ||||
| FACE | |||||
|---|---|---|---|---|---|
| Original | ConvBio | ConvInt | BioInt | All Three | |
| Ind | 79.17 ±4.35 | 79.08 ±4.36 | 79.17 ±4.02 | 78.38 ±4.58 | 78.97 ±2.30 |
| Sum | 85.38 ±3.89 | 86.90 ±3.94 | 86.77 ±3.58 | 86.80 ±4.11 | 87.58 ±1.80 |
| MV | 84.23 ±5.00 | 85.10 ±4.70 | 85.07 ±4.46 | 85.02 ±4.92 | 85.78 ±2.58 |
| NB | 79.98 ±5.37 | 81.32 ±5.36 | 81.30 ±5.45 | 81.22 ±6.02 | 82.12 ±3.81 |
| k-NN | 82.33 ±2.09 | 83.43 ±5.33 | 83.30 ±4.81 | 83.38 ±5.19 | 84.32 ±3.06 |
| SVM | 83.18 ±5.76 | 84.43 ±5.47 | 84.48 ±5.02 | 84.67 ±4.91 | 85.25 ±3.15 |
| VOICE | |||||
| Original | ConvBio | ConvInt | BioInt | All Three | |
| Ind | 78.98 ±6.70 | 80.17 ±2.36 | 77.68 ±5.81 | 78.45 ±5.14 | 78.95 ±4.06 |
| Sum | 84.37 ±3.80 | 88.88 ±3.90 | 85.32 ±6.39 | 87.37 ±6.56 | 91.47 ±4.46 |
| MV | 84.43 ±3.68 | 87.87 ±2.98 | 84.42 ±5.59 | 86.92 ±5.44 | 90.25 ±4.17 |
| NB | 83.40 ±5.07 | 78.70 ±8.13 | 79.28 ±7.61 | 78.82 ±9.68 | 81.43 ±8.87 |
| k-NN | 84.70 ±4.39 | 86.87 ±3.90 | 83.97 ±6.21 | 85.63 ±6.22 | 89.25 ±4.89 |
| SVM | 87.83 ±4.09 | >88.72 ±2.99 | 86.50 ±5.42 | 88.38 ±4.96 | 90.78 ±3.84 |
| FACE+VOICE | |||||
| Original | ConvBio | ConvInt | BioInt | All Three | |
| Ind | 79.12 ±4.51 | 78.60 ±4.12 | 78.68 ±5.66 | 78.60 ±4.92 | 79.10 ±4.74 |
| Sum | 90.82 ±3.13 | 93.65 ±3.73 | 93.33 ±4.32 | 93.70 ±4.03 | 96.02 ±3.12 |
| MV | 90.28 ±3.63 | 92.23 ±3.58 | 92.05 ±4.29 | 92.58 ±3.81 | 94.52 ±3.30 |
| NB | 87.63 ±4.47 | 85.77 ±6.42 | 87.58 ±5.92 | 86.62 ±6.61 | 88.28 ±6.38 |
| k-NN | 89.45 ±3.99 | 90.90 ±4.34 | 90.93 ±4.78 | 91.08 ±4.32 | 93.28 ±3.88 |
| SVM | 91.45 ±3.79 | 92.32 ±3.66 | 92.80 ±4.26 | 93.15 ±3.27 | 94.52 ±3.12 |
Table 5: Accuracy level (%) and standard deviation: all three optimization techniques to select features for the ensemble systems |
|||||






































