Top Links
Journal of Computational Systems Biology
ISSN: 2455-7625
Predicting Multi-Drug Inhibition Interactions based on Signaling Networks and Single Drug Dose-Response Information
Copyright: © 2016 Fang HB. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Related article at Pubmed, Google Scholar
Inhibiting multiple pathways/targets with combination drug therapies is widely used to maximize therapeutic benefit in many diseases. Therapeutic success can often be improved by concurrently and/or sequentially inhibiting multiple pathways/targets by combining drugs with different mechanisms of action. It is critical to understand potential drug interactions in developing and optimizing new multidrug regimens. We used data from experiments of single drugs (and few combinations) and existing signaling network knowledge from sources such as KEGG, to develop a statistical rescaling model to describe the effects of drugs on network topology. The model comprises a Hill equation for signals arriving at each receptor, a generic enzymatic rate equation to transmit signals among connecting genes, and a regression model to represent the cumulative effect of genes implicated in activation of the cell death machinery. We performed in silico experiments to derive a global sensitivity index of each term in the functional ANOVA of the dose-response model by generating doses of the drugs with the Quasi Monte-Carlo method. Only terms with large (principal) global sensitivity indices remain in the functional dose-response model. Thus, we reduce a high dimensional problem into one that can be managed experimentally. The model generates an index that indicates potential interactions of the drugs and the principal combinations, those associated with large global sensitivity indices, can be considered as candidates for further experimental validation.
Keywords: Drug combinations; Drug interactions; Signaling network; Statistical models; Function ANOVA; In silico experiments; Quasi Monte-Carlo
Combination therapy is the hallmark of therapies for cancer, viral or microbial infections, hypertension, and other diseases involving complex biological networks. For example, the transformation of a normal cell to a cancer cell involves multiple genetic mutations and up to 12 pathways [1]. Therefore, therapeutic success can often be improved by concurrently and/or sequentially inhibiting multiple pathways/targets by combining drugs with different mechanisms of action. Synergistic drug combinations, which are more effective than predicted from summing the effects of individual drugs, often achieve increased efficacy with lower doses and have reduced toxicity [2]. Since many molecularly-targeted agents exhibit synergy when used in combination with ≥2 cytotoxic drugs [2,3], significant interest remains in developing quantitative methods to detect drug synergy [4-9]. However, combination drug therapy targeting just a few gene products may be ineffective [4,10,11]. Increasing the number of agents in a combination may provide better outcomes. In the past decade, the approach to cancer therapy has been revolutionized by the identification of a variety of novel signal transduction targets amenable to therapeutic intervention. These targets were identified based on improved understanding of the molecular mechanisms of action of second messengers, other components of signal transduction pathways, and systems biology. These advances have also made available large number of potential agents and call for new quantitative approaches for combination therapy [6,12,13]. Despite the changing paradigm to target multiple pathways, methodological advances in accurately identifying drug interactions have fallen behind, as shown by a paucity of literature on the design and analysis of multi-drug combinations.
The challenge presented by multi-drug combinations is exceptional. For example, with 10 drugs, each with only 3 doses, the number of potential combinations reaches 1,048,545, a high dimensional statistical problem. Even with 5 drugs, the number of combinations is 1008. The exponentially growing number of combinations with even a few selected doses per drug quickly precludes laboratory testing. Despite the biological advances mentioned above and the importance of multi-agent combinations, current methods are mostly topological as opposed to quantitative, and do not account for high dimensionality and proper model assumptions [14,15]. Consequently, many multidrug combination studies use suboptimal experimental design and synergy analysis, where only pairwise combinations are studied and/or the dose of one or more drugs is fixed.
Currently no published methods for screening large number of combinations use both network information and single drug experimental data. One recent attempt to use network information is a search algorithm by Calzolari et al. [16] based on a deterministic model. The method can only accommodate 2 pre-fixed dose levels of each drug with no more than 6 constituent drugs. Furthermore, the method provides neither dose selection nor sufficient information on dose-response, partly because the method ignores the single drug dose-response data that is a prerequisite for drug combination studies. A method is urgently needed to enable optimal experimental design that provides the concentrations or doses of the combinations, and allow an experimentally feasible exploration of the dose-effect surface with the smallest possible sample size. We have developed a novel method to screen the large number of combinations and identify an experimentally manageable experimental design by using the dose-response data for single drugs and pathway/network knowledge to obtain an estimate of the functional structure of the dose-response relationship.
For the purposes of this study, biological networks controlled/regulated by a receptor(s) are viewed as comprising connecting genes and output nodes that are implicated in determining activation of the cell death machinery. Figure 1 presents a typical example network - apoptosis related signaling from the KEGG database (hsa04210). Different nodes have various signal propagation rules. For a given dose-level x = (x1,x2,…xs)T of drugs A1,A2,…AS, denote a0i (x) as the signal of receptor i obtained (i = 1, 2, …, r)and ai (x) as the signal connecting gene i obtained(i = 1, 2, …, r). Gene activity levels often exhibit a non-linear relationship to their upstream regulatory signals. Typically, a Hill equation [17] can be used to model the activity a0i (x)at receptor i,
where αi and βi = (βi1,βi2,….βis)T are the parameters to be estimated. To characterize the transmission of signals among connecting genes, the generic enzymatic rate equations can be used to adjust for possible feedback loops. Such equations have been motivated by various computational and biological considerations, a result of the close interaction between experimental and computational efforts [18,19]. Let aj (x) be the activity at gene j and a(i,j)(x) the signal sending from gene j to gene i. The activity ai(x) at gene i is defined to be the summation of all signals a(i,j)(x) for gene j linked up gene i, and the generic enzymatic rate equation then suggests that
where n(i) is the set of genes that signal to gene i, and ω is the expected steady state parameter. VFj and VBj are the forward and backward parameters, respectively. From the biological point of view, VFj can be interpreted as the steady state biomass flux sent out from gene i when the reaction is forward, while VBj is interpreted as the steady state biomass flux sent out from gene i when the reaction is backward. When the reaction from gene j to gene i is irreversible in the backward direction, VFj = 0. The number of parameters VFj and VBj may become large if many connecting genes exist in the network. The forward and backward parameters VFj and VBj of connecting gene i may differ with those of connecting gene j (i ≠ j). Statistical variations typically occur when signals pass though the network because of link instability, stochastic noise inherent in the signal propagation rules, and/or chaos phenomena from the presence of loops. To model the network efficiently, therefore it is reasonable to assume that and (i = 1,2,…,) are random effects that are independently and identically distributed (i.i.d.) normal random variables with mean µ1 and variance σ12.
A linear model is used to represent the cumulative effect of genes implicated at activation of the cell death machinery. For a given dose-level x = (x1,x2,…xs)T of drugs A1,A2,…AS, let Y(x) be the observed viability and a(x)=(ail(x),…aih(x))T be the vector of the activities at genes i1,….,ih which activate the output, then we have
Where the subscript k is the k-th replication at dose-level x = (x1,x2,…xs)T, ∈k (x)~N(0,(σ(x))2) is the measurement error of the observed data, and the standard deviation σ(x)of the measurement error may depend on the dose-level x = (x1,x2,…xs)T. u0 is the intercept parameter, and u = (u1,..,uh)T is the vector of regression parameters to be estimated. The positive parameter ui indicates promotion by gene i; the negative parameter uj indicates inhibition by gene j.
A training dataset is needed to model the biological network. In combination studies, the data from single drug experiments are usually available a priori. To use the network to discover multi-drug interactions, data from single drug responses cannot ensure the identification of parameters in models (1)-(3). Some limited data on the drug combinations is needed to find a model. The IC50 of each drug can be estimated from the single drug dose-response curves. We recommend a relatively simple experiment of the drug combinations with each drug at its individual IC50. To explore the dose-response in high dimensions, which is not well estimated by the single drug experimental data, experimentally 2s higher order combinations are considered for s drugs. Table 1 provides an example using 10 combinations of 5 drugs. The training dataset then consists of the data from single drug experiments and from limited higher order combination experiments.
Based on the training data, we can estimate the parameters in equations (1)-(3) with the maximum likelihood approach. Let β = (β1T,…, βrT )T, α= (α1,…, αr)T, and θ= (βT, αT, ω, uT, σ02, μ1, σ12)T and be the vector of all parameters to be estimated. Since a(x) in model (3) equals to zero when x = 0, the intercept μ0 should be 100% cell viability if there is no drug intervention on the network.
Suppose that there are n distinct inputs x1,.., xn, and ki replications at each input xi, the corresponding output is Yij for j = 1,2,.., ki; and i = 1,2,…, n. For given μ1, σ12 and a sample VFi and VBi (i =1, 2,…) from the normal distribution N(μ1, σ12 ), the ECM algorithm [20] can be applied to obtain the maximum likelihood estimation of β, α, ω, u, σ02. Furthermore, for given β, α, ω, u, σ02, we can obtain n samples of VFi and VBi using equation (3) with n distinct inputs x1,…, xn. The estimation of μ1 and σ12 can then be obtained. Details for parameter estimation are provided in the Appendix.
After we obtain the estimated parameters in models (1)-(3), the drug dose-response surface y = g(x) can be estimated in silico. A detailed and rigorous definition of a drug dose-response surface can be found in the paper by Kong and Lee [7]. The drug dose-response surface is an (s+1)- dimensional response surface in s drug combinations which is used to describe the dose-effect relationship. In this work, we would not expect the precise drug dose-response surface to be adequately estimated with limited data and in silico experiments. However, we can get sufficient information of drug interactions using the functional ANOVA [21-23], which is similar to functional principal component analysis.
Recall that x = (x1, x2,…xs)T, is the dose-level of s drugs A1, A2,…, AS, and y = g(x) is the corresponding dose-response. Let g0 = ∫[0,1]s g(x)dx be the overall mean of g(x). Then there is a unique decomposition
which satisfies
Moreover, (4) has orthogonal components, i.e., if (i1,…,iu) ≠ (ji,…, jv),
The functions on the right-hand side of the equation (4) are determined by
and so on. From equations (4)-(6), we have
The total and partial variances can be defined by
respectively. Note that The ratios
are called global sensitivity indices [21-23]. The integer k is called the order of the index. All Ri1,…,ikʹs are non-negative and their sum
The equality Ri1,…,ik = 0 implies that gi1,…,ik = 0 and so the interaction of drugs Ai1…Aik is not significant. Significance of the interaction of drugs Ai1…Aikdecreases with decreasing Ri1,…,ik. Hence the dose-response model can be reduced if we only retain the principal terms with the largest global sensitivity indices, an approach similar to principal component analysis. It is also expected that the number of terms in the dose-response functional ANOVA representation will be reduced significantly because the cumulative global sensitivity indices of the first few terms usually contribute a dominant portion (say, 80%) of the total variation [24]. To obtain the numerical values of the global sensitivity indices, the Quasi-Monte Carlo methods for approximating the integrals can be adopted. For more details, please refer to Fang et al. [24].
To illustrate the proposed methods, we consider the apoptosis network (hsa04210) as shown in Figure 1. Two simulation experiments are conducted to investigate the effectiveness of the optimal network simulator for the discovery of multidrug interactions using the apoptosis signaling network. The first example involves a combination study of 5 drugs; the second example considers as many as 10 drugs.
Consider a combination study of 5 drugs A1,…,A5. The dose-levels of A1,…,A5 are denoted by x1,…,x5, respectively. Without loss of generality, assume that x1,…,x5 Є [0,1] . Based on the KEGG network (hsa04210), the “true” dose-response is assumed to be
Where x = (x1,…., x5)T. Decompose the true dose-response (9) using the functional ANOVA representation (7) and (8), the global sensitivity indices are 38.06% for variable term x1x2x3x4, 29.61% for variable term x1, 15.78% for variable term x2 and 8.40% for variable term x3, respectively. The variable terms are ignored if their global sensitivity indices are less than 1%. The response in (9) can then be approximated by
With the relative mean squared prediction error (RMSPE) given by RMSPE = {∫(0,1)5 [(y(x) − y*(x))/y(x)]2 dx} × 100% = 8.25%, which indicates that y*(x) is a good approximation of the true dose-response. The “true” response surface in (9) is mainly contributed by the interaction of A1A2A3A4 and drugs A1, A2 (the total of global sensitivity indices is 83.45%), 236 and the resulting global sensitivity indices are shown in the left pie of Figure 2.
We conducted the simulation experiments to investigate whether our method can identify correctly these true significant single drugs and drug interactions. From equation (9), the single drug dose-responses can be obtained by setting other variables to zero. For each drug, 8 concentration levels {0.0100; 0.0193; 0.0372; 0.0717; 0.1382; 0.2664; 0.5135; 0.9900} are chosen and 8 replications at each concentration with the random error ε ~ N(0,1). The generated data of single drug experiments are listed in Table S1 (Supplement).
From the single drug dose-responses, the respective IC50 of each drug is estimated to be 0.07, 0.10, 0.14, 0.19, and 0.26 for drugs A1, A2, A3, A4 and A5. To generate the data of drug combinations, 10 mixtures as shown in Table 1 are chosen and three replications at each mixture with the random error ε ~ N(0,1). Data generated from combination experiments are listed in Table S2 of Supplement.
Based on the training data, we obtained the parameter estimation for models (1)-(3), and then the dose-response function y = g(x) can be simulated for any dose-level x = (x1,…,x5)T Є [0,1]5 of drugs A1,…..,A5. To estimate the global sensitivity index Ri1,…,ik, the Quasi Monte-Carlo method is used because of its improved efficiency, fast convergent rates in approximating the integrals [25,26]. With the Quasi Monte-Carlo method, we generate a set of 5-dimensional points {x(j) : j = 1,2,…,N}, which is space filling over the experimental domain [0,1]5. With properly chosen x(j) s, e.g., the uniformly scattered points, the quantity
converges to Di1,…,ik much faster (O(N-1(logN)5-1)) than randomly generated x(j) s(O(N-1/2)). Hence, we can obtain the estimates of all global sensitivity indices Ri1,…,ik. In this simulation, 10,000
To further illustrate the proposed methods, we considered a combination study using more drugs for the simulation. The dose-levels of 10 drugs A1,….., A10 are denoted by x1,……x5, respectively. Based on the KEGG network (hsa04210), the “true” dose-response is assumed to be
where x = (x1,…,x10)T Є [0,1]10. Decompose the true dose-response (12) using the functional ANOVA representation (7) and (8), the global sensitivity indices are 41.69% for variable term x1x2x3x4x5 21.23% for variable term x1x2x3x4x5x6x7, 11.90% for variable term x1x2x3, 11.01% for variable term x1, and 7.21% for variable term x2, respectively. The variable terms are ignored if their global sensitivity indices are less than 1%. The response in (12) can then be approximated by
with RMSPE = 5.21%, which indicates that y*(x) provides a good approximation of the true dose-response. Thus, the “true” response surface in (12) is mainly contributed by the interaction of A1A2A3A4A5A6A7, A1A2A3A4A5, A1A2A3 and drug A1 (the total of global sensitivity indices is 85.83%); the resulting global sensitivity indices are shown in the left pie of Figure 3.
Simulation experiments are conducted to investigate whether our method can correctly identify these true significant single drugs and drug interactions in this setting. From equation (12), the single drug dose-responses can be obtained by setting other variables to zero. The corresponding IC50 of each drug is estimated to be 0.07, 0.08, 0.10, 0.11, 0.14, 0.16, 0.19, 0.22, 0.26, and 0.31 for drugs A1, …, A10, respectively. For each drug, 8 concentration levels {0.01; 0.02; 0.04; 0.07; 0.14; 0.27; 0.51; 0.99} are chosen with 8 replications at each concentration with the random error ε ~ N(0,1). The data generated for the single drug experiments are listed in Table S3 (Supplement). To generate the data for drug combinations, 20 mixtures are chosen with three replications at each mixture with the random error ε ~ N(0,1) , and the corresponding data of combination experiments are listed in Table S4 of the Supplement.
Similar to Simulation 1, the estimation of parameters in models (1)-(3) is obtained using the training data. In this simulation, 10,000 Quasi Monte-Carlo samples are generated and the estimation of the global sensitivity indices is repeated 100 times. The average of the estimated global sensitivity indices (and their corresponding standard deviations) are shown in the right pie of Figure 3. The small standard deviations indicate that the integrations are at convergence. On average, 45.39% global sensitivity index for variable term x1x2x3x4x5, 25.91% for variable term x1x2x3x4x5x6x7, 9.27% for variable term x1x2x3, and 8.97% for variable term x1, respectively. The results show that for the dose-response of the 10 drug combinations, the most significant contributions are the interactions of of A1A2A3A4A5, A1A2A3A4A5A6A7, A1A2A3 and drug of A1 (the total of global sensitivity indices is about 90%), which is also consistent with the global sensitivity indices from the true dose-response.
To get an idea of the computing efficiency of the proposed method, Table 2 below provides the CUP times for Simulations 1 and 2. The CUP time for each simulation can be divided into two parts: the first part is for the ECM algorithm (parameter estimation), the second part is for the functional ANOVA (integral calculation). It can be seen from Table 2 that the 10-drug simulation is much more time-consuming than the 5-drug simulation. However, the CPU time for the 10-drug simulation is still acceptable, say that about 1 hour for the ECM algorithm and about 5 minutes for the functional ANOVA on a regular PC.
Cancer cells carry out their functions following appropriate responses to the extracellular and intracellular inputs to their complex network of signaling pathways. Many genes that code for proteins in these pathways are controlled by regulatory proteins that up-regulate or down regulate these genes depending on the inputs to the signaling network. Though striking progress is being made in extracting networks using a range of experimental data [27,28], knowledge of signaling networks remains predominantly at the level of topology rather than details on the rate constants and nonlinear message passing that occurs within the networks. Models to distinguish between members of a population of cells, for example, different cancer cells from different normal tissue types, require differences in message passing parameters and/or expression levels of the genes in the network.
Using data from experiments with single drugs (and some drug combinations) and the existing network information, we proposed statistical models to describe the drug effects on the network. Through these statistical models, we conducted computer experiments (in silico) to derive a global sensitivity index of each term in the functional ANOVA of dose-response model by generating doses of the drugs with the Quasi Monte-Carlo method. Then, we can predict the main effects that occur with combinations of multiple drugs. Two simulation studies illustrate the superior performance of our methods. The principal global sensitivity indices generally select 3 to 4 terms of multidrug combinations in the functional ANOVA model if the true dose-response function is smooth. Therefore, the model generates an index that indicates potential interactions of the drugs and the principal combinations, those associated with large global sensitivity indices, can be considered as candidates for further experimental validation.
In some signaling networks there may be loops due to feedback links among genes. Several procedures can simulate signal propagation passing networks with loops [29-31]. For any specific loop, an effective algorithm for optimal signaling with feedback loops should be developed. Furthermore, to investigate drug interactions it is important to understand the mechanisms of each drug in drug combination studies. If the relationships among drugs and receptors/or genes are known, the number of parameters in models (1)-(3) can be decreased, and some constraints can be applied to achieve high prediction accuracy. It is worth noting that the number of parameters in our network model is usually large even there are some constraints on them. The large number of parameters may cause over-fitting. One possible solution to address the potential over-fitting problem is to use the penalized likelihood approach or regularized regression machine learning, i.e., a penalty function such as Lasso [32] or SCAD [33] can be added to (A3) to achieve sparse estimation.
In this paper we have developed a novel method to screen the large number of combinations and identify an experimentally manageable experimental design by using the dose-response data for single drugs and pathway/network knowledge to obtain an estimate of the functional structure of the dose-response relationship. It is highly beneficial in bringing forth a framework for selecting drug interactions, and developing experimental designs and statistical procedures to estimate the high dimensional dose-response surface.
The authors are grateful to the reviewer for his/her constructive comments. The research of Drs. Fang, Huang and Tan is partially supported by the National Cancer Institute (NCI) grant R01CA164717. Dr. Clarke’s research is supported in part by NCI system biology grant 5U54CA149147.
The authors declare that they have no competing interests.
HBF has contributed to the problem formulation, developing the statistical models, and writing the manuscript. HH has contributed to data analysis, implementing and simulating the models. RC has contributed to the problem formulation, and writing the manuscript. MT has contributed to the problem formulation, developing the statistical methods and writing the manuscript. All authors have read and approved the final version of the manuscript.
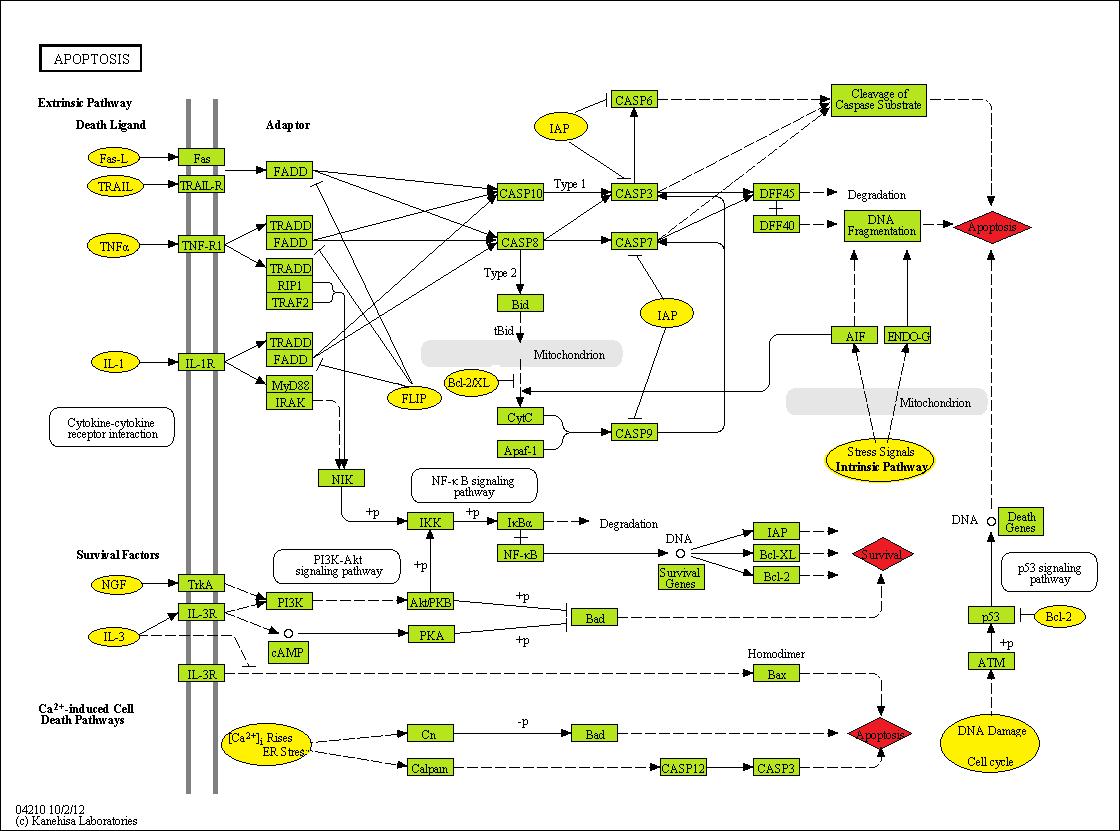 |
| Figure 1: The human apoptosis network extracted from the KEGG database (hsa04210). Genes are categorized as receptors (yellow circles), connecting genes (green rectangles), and the output nodes (red diamonds) that are implicated at the onset of the cell death machinery. A solid line with an arrow at the end indicates direct promotion; a dashed line with an arrow at the end indicates indirect promotion; a dashed line with a bar at the end indicates inhibition. A cross symbol between two genes indicates dissociation, in which case the two genes may be viewed as a single node (e.g., DFF45 and DFF40) |
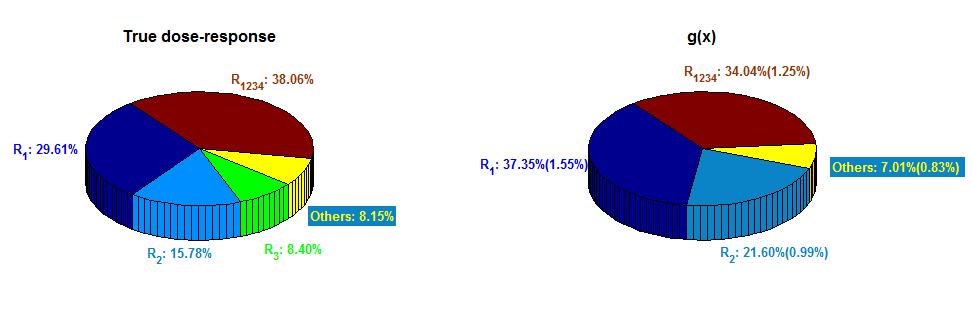 |
| Figure 2: Global sensitivity indices in Simulation 1. Left: global sensitivity indices of the true dose- response; Right: estimated global sensitivity indices of the predicted dose-response and their standard deviations in the parentheses |
 |
| Figure 3: Global sensitivity indices in Simulation 2. Left: global sensitivity indices of the true dose- response; Right: estimated global sensitivity indices of the predicted dose-response and their standard deviations in the parentheses |
Drug |
mixture 1 |
mixture 2 |
mixture 3 |
mixture 4 |
mixture 5 |
mixture 6 |
mixture 7 |
mixture 8 |
mixture 9 |
mixture 10 |
A1 |
IC50 |
IC50 |
IC50 |
IC50 |
IC50 |
0 |
IC50 |
0 |
0 |
0 |
A2 |
IC50 |
IC50 |
IC50 |
IC50 |
0 |
IC50 |
0 |
IC50 |
IC50 |
IC50 |
A3 |
IC50 |
IC50 |
IC50 |
0 |
IC50 |
IC50 |
IC50 |
0 |
IC50 |
IC50 |
A4 |
IC50 |
IC50 |
0 |
IC50 |
IC50 |
IC50 |
0 |
IC50 |
0 |
IC50 |
A5 |
IC50 |
0 |
IC50 |
IC50 |
IC50 |
IC50 |
IC50 |
IC50 |
IC50 |
0 |
Table 1: 10 mixtures chosen for the combination experiments of 5 drugs |
||||||||||
ECM algorithm |
Functional ANOVA |
|
Simulation 1 (5 drugs) |
985.6s |
8.8s |
Simulation 2 (10 drugs) |
4052.3s |
300.6s |
• The stop error for ECM algorithm is 0.01 |
||
x1 |
x2 |
x3 |
x4 |
x5 |
y1 |
y2 |
y3 |
y4 |
y5 |
y6 |
y7 |
y8 |
y |
0.01 |
0 |
0 |
0 |
0 |
78.45 |
77.61 |
80.25 |
79.01 |
78.46 |
79.32 |
80.11 |
80.11 |
79.17 |
0.02 |
0 |
0 |
0 |
0 |
68.03 |
69.42 |
69.36 |
67.21 |
69.51 |
69.3 |
70.69 |
69.52 |
69.13 |
0.04 |
0 |
0 |
0 |
0 |
59.13 |
58.56 |
58.73 |
58.4 |
59.99 |
58.78 |
59.43 |
58.61 |
58.95 |
0.07 |
0 |
0 |
0 |
0 |
48.11 |
49.44 |
48.06 |
50.15 |
49.63 |
48.31 |
51.28 |
50.1 |
49.39 |
0.14 |
0 |
0 |
0 |
0 |
39.67 |
40.03 |
39.85 |
39.64 |
41.42 |
40.01 |
39.85 |
38.31 |
39.85 |
0.27 |
0 |
0 |
0 |
0 |
29.28 |
28.94 |
30.66 |
28.73 |
29.24 |
28.5 |
28.61 |
30.09 |
29.26 |
0.51 |
0 |
0 |
0 |
0 |
22.18 |
19.71 |
19.7 |
19.37 |
19.26 |
19.97 |
17.8 |
20.81 |
19.72 |
0.99 |
0 |
0 |
0 |
0 |
11.29 |
10.5 |
9.61 |
10.4 |
8.4 |
11.48 |
9.82 |
10.36 |
10.23 |
0 |
0.01 |
0 |
0 |
0 |
81.58 |
82.24 |
83.77 |
83.09 |
84.99 |
83.66 |
84.79 |
84.96 |
83.63 |
0 |
0.02 |
0 |
0 |
0 |
74.67 |
75.27 |
73.13 |
75.21 |
75.1 |
74.09 |
74.55 |
76.27 |
74.79 |
0 |
0.04 |
0 |
0 |
0 |
62.99 |
66.81 |
63.89 |
63.74 |
64.3 |
65.28 |
64.8 |
65.31 |
64.64 |
0 |
0.07 |
0 |
0 |
0 |
54.28 |
55.5 |
54.36 |
56.35 |
55.44 |
54.24 |
53.96 |
54.81 |
54.87 |
0 |
0.14 |
0 |
0 |
0 |
44.86 |
44.38 |
44.74 |
43.61 |
44.88 |
45.72 |
44.84 |
45.33 |
44.79 |
0 |
0.27 |
0 |
0 |
0 |
35.59 |
35.27 |
34.78 |
35.04 |
35.14 |
34.5 |
33.21 |
35.27 |
34.85 |
0 |
0.51 |
0 |
0 |
0 |
24.73 |
23.96 |
25.61 |
23.48 |
25.11 |
26.01 |
24.24 |
23.68 |
24.6 |
0 |
0.99 |
0 |
0 |
0 |
16.73 |
17.03 |
15.26 |
14.43 |
15.59 |
15.78 |
14.33 |
14.73 |
15.49 |
0 |
0 |
0.01 |
0 |
0 |
88.6 |
90.02 |
90.89 |
88.48 |
89.18 |
88.87 |
89.6 |
90.3 |
89.49 |
0 |
0 |
0.02 |
0 |
0 |
79.56 |
80.02 |
79.54 |
79.63 |
82.02 |
78.37 |
79.22 |
79.19 |
79.69 |
0 |
0 |
0.04 |
0 |
0 |
70.05 |
68.51 |
71.19 |
70.33 |
68.22 |
68.34 |
68.23 |
69.97 |
69.35 |
0 |
0 |
0.07 |
0 |
0 |
59.62 |
59.86 |
58.81 |
59.84 |
57.68 |
59.27 |
59.53 |
58.53 |
59.14 |
0 |
0 |
0.14 |
0 |
0 |
50.57 |
49.13 |
50.22 |
49.32 |
48.55 |
49.25 |
49 |
49.76 |
49.48 |
0 |
0 |
0.27 |
0 |
0 |
40.17 |
39.53 |
39.58 |
40.66 |
38.75 |
39.44 |
39.18 |
40.44 |
39.72 |
0 |
0 |
0.51 |
0 |
0 |
29.21 |
29.43 |
30.6 |
30.8 |
29.56 |
30.98 |
30.86 |
28.64 |
30.01 |
0 |
0 |
0.99 |
0 |
0 |
18.35 |
19.13 |
20.75 |
20.27 |
19.98 |
19.85 |
20.26 |
20.5 |
19.89 |
0 |
0 |
0 |
0.01 |
0 |
95.94 |
93.17 |
91.89 |
94.65 |
93.86 |
95.22 |
94.48 |
93.89 |
94.14 |
0 |
0 |
0 |
0.02 |
0 |
83.63 |
84.02 |
82.9 |
84.64 |
84.77 |
83.7 |
85.11 |
83.29 |
84.01 |
0 |
0 |
0 |
0.04 |
0 |
74.49 |
72.68 |
72.94 |
73.4 |
74.77 |
75.36 |
74.56 |
74.35 |
74.07 |
0 |
0 |
0 |
0.07 |
0 |
65.1 |
65.14 |
64.94 |
65.3 |
65.29 |
64.01 |
65.09 |
62.64 |
64.69 |
0 |
0 |
0 |
0.14 |
0 |
54.8 |
54.57 |
56.16 |
54.03 |
56.47 |
54.87 |
55.37 |
52.56 |
54.85 |
0 |
0 |
0 |
0.27 |
0 |
43.94 |
45.54 |
44.52 |
44.24 |
46.07 |
45.81 |
46.01 |
43.67 |
44.97 |
0 |
0 |
0 |
0.51 |
0 |
34.53 |
35.27 |
35.81 |
35.17 |
33.71 |
34.58 |
35.47 |
34.01 |
34.82 |
0 |
0 |
0 |
0.99 |
0 |
25.03 |
25.64 |
25.7 |
24.84 |
22.82 |
24.71 |
26.56 |
23.98 |
24.91 |
0 |
0 |
0 |
0 |
0.01 |
100.56 |
97.59 |
98.03 |
98.95 |
99.98 |
101.08 |
99.1 |
97.35 |
99.08 |
0 |
0 |
0 |
0 |
0.02 |
88.37 |
88.21 |
89.63 |
89.83 |
87.4 |
90.18 |
89.18 |
89.52 |
89.04 |
0 |
0 |
0 |
0 |
0.04 |
80.17 |
78.94 |
78.63 |
80.43 |
79.45 |
78.95 |
81.09 |
77.79 |
79.43 |
0 |
0 |
0 |
0 |
0.07 |
69.85 |
69.65 |
71.05 |
69.34 |
69.57 |
70.19 |
69.03 |
69.65 |
69.79 |
0 |
0 |
0 |
0 |
0.14 |
59.46 |
60.82 |
59.66 |
60.02 |
61.92 |
59.33 |
59.69 |
60.48 |
60.17 |
0 |
0 |
0 |
0 |
0.27 |
48.79 |
49.55 |
51.48 |
49.61 |
49.77 |
50.55 |
50.76 |
49.84 |
50.04 |
0 |
0 |
0 |
0 |
0.51 |
39.71 |
41.26 |
39.57 |
40.23 |
39.49 |
41.41 |
40.15 |
40.09 |
40.24 |
0 |
0 |
0 |
0 |
0.99 |
30.06 |
30.63 |
30.74 |
30.59 |
30.39 |
28.55 |
31.56 |
29.77 |
30.29 |
The column labella “xi” contains the experimental levels of drug Ai, i = 1,…,5 |
|||||||||||||
x1 |
x2 |
x3 |
x4 |
x5 |
y1 |
y2 |
y3 |
y |
|||||
0.07 |
0 |
0.14 |
0 |
0.26 |
42.59 |
41.31 |
41.99 |
41.96 |
|||||
0 |
0.1 |
0.14 |
0.19 |
0 |
33.92 |
36.13 |
34.54 |
34.87 |
|||||
0 |
0.1 |
0.14 |
0 |
0.26 |
40.73 |
41.09 |
40.83 |
40.89 |
|||||
0 |
0.1 |
0 |
0.19 |
0.26 |
34.99 |
33.52 |
33.81 |
34.11 |
|||||
0.07 |
0.1 |
0.14 |
0.19 |
0 |
30.69 |
29.29 |
29.07 |
29.68 |
|||||
0.07 |
0.1 |
0.14 |
0 |
0.26 |
35.89 |
33.31 |
36.15 |
35.12 |
|||||
0.07 |
0.1 |
0 |
0.19 |
0.26 |
29.6 |
28.86 |
28.04 |
28.83 |
|||||
0.07 |
0 |
0.14 |
0.19 |
0.26 |
33.17 |
33.78 |
33.4 |
33.45 |
|||||
0 |
0.1 |
0.14 |
0.19 |
0.26 |
32.8 |
32.99 |
33.45 |
33.08 |
|||||
0.07 |
0.1 |
0.14 |
0.19 |
0.26 |
29.31 |
29.66 |
29.83 |
29.6 |
|||||
The column labella “xi” contains the experimental levels of drug Ai, i = 1,…,5 |
|||||||||||||
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
x8 |
x9 |
x10 |
y1 |
y2 |
y3 |
y4 |
y5 |
y6 |
y7 |
y8 |
y |
0.01 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
79.93 |
79.57 |
79.11 |
77.59 |
78.85 |
79.33 |
78.55 |
79.85 |
79.1 |
0.02 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
70.1 |
69.59 |
71.1 |
68.78 |
68.32 |
68.51 |
67.95 |
69.5 |
69.23 |
0.04 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
62.69 |
59.56 |
60.3 |
60.37 |
59.08 |
58.92 |
60.07 |
60.09 |
60.13 |
0.07 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
49.86 |
50.15 |
50.36 |
48.4 |
48.45 |
49.94 |
50.33 |
49.7 |
49.65 |
0.14 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
37.63 |
38.97 |
38.74 |
39.15 |
40.08 |
39.78 |
41.02 |
40.15 |
39.44 |
0.27 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
29.9 |
29.89 |
29.87 |
29.98 |
29.75 |
30.19 |
30.4 |
29.27 |
29.91 |
0.51 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
19.65 |
18.27 |
20.09 |
19.32 |
18.21 |
18.31 |
18.68 |
18.5 |
18.88 |
0.99 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
9.02 |
10.82 |
9.85 |
8.92 |
9.86 |
10.22 |
11.43 |
9.59 |
9.96 |
0 |
0.01 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
82.22 |
82.7 |
82.03 |
83.93 |
81.84 |
81.76 |
81.22 |
82.98 |
82.33 |
0 |
0.02 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
72.09 |
71.65 |
72.51 |
71.17 |
70.75 |
71.09 |
71.43 |
72.34 |
71.63 |
0 |
0.04 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
63.95 |
63.73 |
63.32 |
62.11 |
61.14 |
61.17 |
61.91 |
62.2 |
62.44 |
0 |
0.07 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
51.82 |
53.31 |
52.3 |
51.86 |
52 |
52.87 |
50.65 |
52.39 |
52.15 |
0 |
0.14 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
43.11 |
40.37 |
43.46 |
41.26 |
40.04 |
41.02 |
42.39 |
41.75 |
41.67 |
0 |
0.27 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
34.37 |
30.3 |
30.09 |
31.87 |
31.3 |
31.58 |
34.03 |
34.25 |
32.22 |
0 |
0.51 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
21.41 |
21.74 |
21.79 |
22.23 |
22.68 |
21.78 |
21.66 |
23.18 |
22.06 |
0 |
0.99 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
12.3 |
14.57 |
13.24 |
11.23 |
12.6 |
15.25 |
12.68 |
10.16 |
12.75 |
0 |
0 |
0.01 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
84.98 |
83.75 |
85.66 |
84.32 |
83.7 |
83.54 |
82.47 |
84.92 |
84.17 |
0 |
0 |
0.02 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
75.27 |
73.93 |
73.78 |
73.99 |
72.71 |
73.9 |
75.75 |
74.75 |
74.26 |
0 |
0 |
0.04 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
65.59 |
64.84 |
66.49 |
63.37 |
65.07 |
63.94 |
64.11 |
65.43 |
64.85 |
0 |
0 |
0.07 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
52.8 |
54.66 |
55.71 |
53.88 |
55.26 |
56.04 |
53.8 |
54.75 |
54.61 |
0 |
0 |
0.14 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
45.51 |
44.18 |
47.52 |
47.1 |
43.64 |
44.5 |
45.19 |
43.35 |
45.12 |
0 |
0 |
0.27 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
35.92 |
36.38 |
35.14 |
35.48 |
35.81 |
33.02 |
34.85 |
34.03 |
35.08 |
0 |
0 |
0.51 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
25.19 |
24.91 |
25.24 |
25.85 |
25.65 |
24.19 |
22.61 |
22.59 |
24.53 |
0 |
0 |
0.99 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
16.25 |
15.01 |
16.32 |
13.9 |
16.31 |
15 |
16.47 |
15.92 |
15.65 |
0 |
0 |
0 |
0.01 |
0 |
0 |
0 |
0 |
0 |
0 |
85.86 |
88.1 |
86.99 |
86.54 |
85.61 |
86.93 |
87.8 |
85.72 |
86.69 |
0 |
0 |
0 |
0.02 |
0 |
0 |
0 |
0 |
0 |
0 |
76.42 |
76.54 |
78.31 |
77.13 |
78.09 |
76.36 |
78.8 |
76.25 |
77.24 |
0 |
0 |
0 |
0.04 |
0 |
0 |
0 |
0 |
0 |
0 |
66.67 |
65.7 |
66.82 |
67.28 |
67.41 |
67.24 |
67.35 |
66.47 |
66.87 |
0 |
0 |
0 |
0.07 |
0 |
0 |
0 |
0 |
0 |
0 |
58.51 |
58.1 |
56.9 |
56.94 |
57.74 |
56.82 |
59.85 |
57.37 |
57.78 |
0 |
0 |
0 |
0.14 |
0 |
0 |
0 |
0 |
0 |
0 |
47.3 |
47.59 |
47.21 |
48.03 |
48.14 |
47.89 |
45.82 |
46.86 |
47.35 |
0 |
0 |
0 |
0.27 |
0 |
0 |
0 |
0 |
0 |
0 |
36.95 |
34.48 |
38.85 |
37.74 |
38.35 |
37.72 |
38.08 |
37.15 |
37.41 |
0 |
0 |
0 |
0.51 |
0 |
0 |
0 |
0 |
0 |
0 |
25.51 |
28.72 |
26.82 |
27.68 |
29.35 |
29.06 |
28.21 |
28.22 |
27.95 |
0 |
0 |
0 |
0.99 |
0 |
0 |
0 |
0 |
0 |
0 |
19.84 |
16.87 |
19.24 |
15.7 |
16.45 |
17.09 |
18.41 |
17.93 |
17.69 |
0 |
0 |
0 |
0 |
0.01 |
0 |
0 |
0 |
0 |
0 |
89.82 |
87.44 |
89.69 |
89.83 |
89.3 |
87.53 |
89.48 |
88.62 |
88.96 |
0 |
0 |
0 |
0 |
0.02 |
0 |
0 |
0 |
0 |
0 |
80.46 |
77.69 |
79.44 |
79.54 |
77.82 |
76.73 |
79.12 |
79.41 |
78.78 |
0 |
0 |
0 |
0 |
0.04 |
0 |
0 |
0 |
0 |
0 |
70.67 |
68.22 |
69.06 |
68.62 |
70.08 |
69.3 |
69.74 |
68.88 |
69.32 |
0 |
0 |
0 |
0 |
0.07 |
0 |
0 |
0 |
0 |
0 |
59.86 |
58.19 |
60.54 |
59.37 |
58.35 |
61.32 |
59.34 |
59.8 |
59.6 |
0 |
0 |
0 |
0 |
0.14 |
0 |
0 |
0 |
0 |
0 |
50.01 |
51.18 |
49.48 |
49.04 |
48.42 |
48.99 |
49.54 |
47.91 |
49.32 |
0 |
0 |
0 |
0 |
0.27 |
0 |
0 |
0 |
0 |
0 |
39.35 |
40.99 |
39.77 |
41.36 |
40.6 |
40.38 |
39.79 |
38.36 |
40.07 |
0 |
0 |
0 |
0 |
0.51 |
0 |
0 |
0 |
0 |
0 |
28.87 |
29.84 |
31.37 |
30.41 |
29.07 |
30.65 |
31.03 |
28.47 |
29.96 |
0 |
0 |
0 |
0 |
0.99 |
0 |
0 |
0 |
0 |
0 |
20.27 |
21.95 |
21.72 |
20.36 |
20.32 |
21.33 |
21.2 |
19.92 |
20.88 |
0 |
0 |
0 |
0 |
0 |
0.01 |
0 |
0 |
0 |
0 |
91.24 |
92.4 |
90.73 |
91.78 |
91.45 |
91.25 |
91.88 |
92.14 |
91.61 |
0 |
0 |
0 |
0 |
0 |
0.02 |
0 |
0 |
0 |
0 |
82.18 |
82.89 |
80.1 |
81.75 |
80.93 |
80.7 |
81.61 |
81.75 |
81.49 |
0 |
0 |
0 |
0 |
0 |
0.04 |
0 |
0 |
0 |
0 |
72.14 |
71.86 |
75.51 |
71.69 |
70.63 |
72.83 |
72.36 |
72.22 |
72.03 |
0 |
0 |
0 |
0 |
0 |
0.07 |
0 |
0 |
0 |
0 |
61.46 |
64.67 |
61.1 |
60.91 |
62.35 |
63.68 |
62.04 |
61.39 |
62.2 |
0 |
0 |
0 |
0 |
0 |
0.14 |
0 |
0 |
0 |
0 |
53.32 |
51.65 |
51.35 |
50.42 |
52.25 |
50.75 |
52.9 |
52.56 |
51.9 |
0 |
0 |
0 |
0 |
0 |
0.27 |
0 |
0 |
0 |
0 |
43.82 |
42.81 |
41.57 |
42.76 |
43.58 |
44.11 |
43.64 |
43.33 |
43.2 |
0 |
0 |
0 |
0 |
0 |
0.51 |
0 |
0 |
0 |
0 |
37.79 |
31.32 |
32.77 |
32.87 |
30.73 |
34.03 |
32.14 |
32.54 |
32.4 |
0 |
0 |
0 |
0 |
0 |
0.99 |
0 |
0 |
0 |
0 |
22.91 |
22.93 |
24.59 |
23.5 |
22.94 |
23.1 |
21.99 |
22.74 |
23.09 |
0 |
0 |
0 |
0 |
0 |
0 |
0.01 |
0 |
0 |
0 |
93.89 |
95.52 |
92.99 |
95.3 |
94.04 |
95.08 |
95.4 |
94.92 |
94.64 |
0 |
0 |
0 |
0 |
0 |
0 |
0.02 |
0 |
0 |
0 |
85.85 |
84.19 |
84.68 |
84.77 |
85.4 |
86.41 |
86.16 |
86.23 |
85.46 |
0 |
0 |
0 |
0 |
0 |
0 |
0.04 |
0 |
0 |
0 |
74.02 |
73.97 |
75.37 |
74.09 |
75.58 |
75.94 |
74.98 |
73.74 |
74.71 |
0 |
0 |
0 |
0 |
0 |
0 |
0.07 |
0 |
0 |
0 |
63.57 |
63.35 |
64.28 |
64.3 |
64.34 |
63.55 |
63.56 |
65 |
63.99 |
0 |
0 |
0 |
0 |
0 |
0 |
0.14 |
0 |
0 |
0 |
56.97 |
57.02 |
55.83 |
54.24 |
55.09 |
53.19 |
55.41 |
52.81 |
55.07 |
0 |
0 |
0 |
0 |
0 |
0 |
0.27 |
0 |
0 |
0 |
46.18 |
44.32 |
43.92 |
46.14 |
44.7 |
46.46 |
44.58 |
47.04 |
45.42 |
0 |
0 |
0 |
0 |
0 |
0 |
0.51 |
0 |
0 |
0 |
35.65 |
36.91 |
33.52 |
36.39 |
34.55 |
33.43 |
35.07 |
36.34 |
35.23 |
0 |
0 |
0 |
0 |
0 |
0 |
0.99 |
0 |
0 |
0 |
25.03 |
25.24 |
24.14 |
24.72 |
24.85 |
23.77 |
24.89 |
25.87 |
24.81 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0.01 |
0 |
0 |
94.83 |
98.18 |
96.96 |
96.8 |
96.58 |
97.13 |
96.15 |
96.85 |
96.69 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0.02 |
0 |
0 |
85.73 |
86.87 |
85.42 |
86.34 |
87.7 |
88.34 |
86.03 |
85.57 |
86.5 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0.04 |
0 |
0 |
76.92 |
77.21 |
76.88 |
76.81 |
77.96 |
77.18 |
77.56 |
77.03 |
77.19 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0.07 |
0 |
0 |
67.69 |
66.79 |
66.61 |
65.92 |
67.26 |
68.59 |
65.04 |
68.62 |
67.06 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0.14 |
0 |
0 |
55.8 |
57.95 |
57.7 |
55.96 |
56.54 |
56.63 |
56.17 |
58.22 |
56.87 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0.27 |
0 |
0 |
46.07 |
46.69 |
46.69 |
47.26 |
47.75 |
48.16 |
47.6 |
45.85 |
47.01 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0.51 |
0 |
0 |
38.1 |
38.13 |
37.62 |
37.21 |
37.86 |
36.94 |
37.73 |
39.15 |
37.84 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0.99 |
0 |
0 |
28.42 |
28.13 |
29.13 |
26.73 |
26.32 |
28.09 |
27.56 |
28.69 |
27.88 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0.01 |
0 |
99.39 |
99.88 |
97.62 |
99.92 |
98.57 |
99.13 |
97.71 |
97.75 |
98.75 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0.02 |
0 |
87.46 |
88.61 |
89.35 |
88.75 |
88.64 |
90.83 |
89.77 |
88.46 |
88.98 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0.04 |
0 |
79.4 |
77.52 |
79.73 |
79.91 |
77.28 |
79.2 |
77.38 |
78.33 |
78.59 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0.07 |
0 |
69.68 |
67.35 |
70.43 |
68.31 |
70.65 |
71.84 |
69.28 |
70.3 |
69.73 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0.14 |
0 |
60.82 |
62.4 |
59.03 |
60.58 |
61.74 |
59.15 |
58.79 |
59.7 |
60.28 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0.27 |
0 |
50.07 |
49.72 |
49.68 |
49.3 |
48.33 |
49.26 |
50.76 |
50.61 |
49.72 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0.51 |
0 |
38.82 |
39.72 |
39.65 |
40.69 |
40.86 |
38.02 |
40.47 |
37.27 |
39.44 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0.99 |
0 |
32.25 |
28.69 |
29.77 |
30.9 |
28.71 |
28.85 |
30.63 |
30.12 |
29.99 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0.01 |
99.93 |
99.05 |
98.46 |
98.82 |
99.04 |
99.7 |
99.42 |
99.91 |
99.42 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0.02 |
91.42 |
93.51 |
92.25 |
91.98 |
92.08 |
93.02 |
90.88 |
90.69 |
91.98 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0.04 |
80.96 |
81.84 |
79.8 |
81.46 |
82.55 |
82.83 |
81.22 |
82.88 |
81.69 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0.07 |
72.57 |
73.04 |
72.16 |
72.39 |
71.72 |
73.05 |
73.64 |
72.09 |
72.58 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0.14 |
63.25 |
61.1 |
61.81 |
61.46 |
61.5 |
61.78 |
61.41 |
63.37 |
61.96 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0.27 |
52.18 |
52.59 |
52.15 |
51.64 |
49.94 |
54.16 |
50.94 |
54.12 |
52.22 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0.51 |
42.29 |
41.76 |
39.96 |
43.25 |
43.25 |
41.3 |
42.22 |
40.76 |
41.71 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0.99 |
32.08 |
31.6 |
33.03 |
32.46 |
32.46 |
32.35 |
32.51 |
34.23 |
32.53 |
The column labella “xi” contains the experimental levels of drug Ai, i = 1,…,10 |
||||||||||||||||||
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
x8 |
x9 |
x10 |
y1 |
y2 |
y3 |
y |
0 |
0.08 |
0.1 |
0.11 |
0.14 |
0 |
0.19 |
0.22 |
0.26 |
0.31 |
19.5 |
19.06 |
18.55 |
19.04 |
0.07 |
0 |
0.1 |
0.11 |
0.14 |
0.16 |
0.19 |
0.22 |
0.26 |
0 |
18.25 |
18.59 |
19.19 |
18.68 |
0.07 |
0.08 |
0.1 |
0 |
0.14 |
0.16 |
0 |
0.22 |
0.26 |
0.31 |
18.19 |
19.23 |
17.7 |
18.37 |
0.07 |
0.08 |
0 |
0.11 |
0 |
0.16 |
0.19 |
0.22 |
0.26 |
0.31 |
16.96 |
19.66 |
17.71 |
18.11 |
0.07 |
0.08 |
0.1 |
0 |
0.14 |
0.16 |
0.19 |
0.22 |
0 |
0.31 |
18.15 |
20.58 |
18.14 |
18.96 |
0 |
0.08 |
0.1 |
0.11 |
0.14 |
0.16 |
0.19 |
0 |
0.26 |
0.31 |
18.53 |
17.99 |
16.56 |
17.69 |
0.07 |
0.08 |
0 |
0.11 |
0.14 |
0 |
0.19 |
0.22 |
0.26 |
0.31 |
17.18 |
17.37 |
18.04 |
17.53 |
0.07 |
0 |
0.1 |
0.11 |
0.14 |
0.16 |
0.19 |
0.22 |
0 |
0.31 |
18.94 |
17.09 |
18.37 |
18.13 |
0.07 |
0.08 |
0.1 |
0.11 |
0 |
0.16 |
0.19 |
0.22 |
0.26 |
0 |
18.33 |
18.3 |
16.99 |
17.87 |
0 |
0.08 |
0.1 |
0.11 |
0.14 |
0.16 |
0.19 |
0.22 |
0.26 |
0.31 |
16.39 |
16.11 |
16.27 |
16.26 |
0.07 |
0 |
0.1 |
0.11 |
0.14 |
0.16 |
0.19 |
0.22 |
0.26 |
0.31 |
14.33 |
16.71 |
16.24 |
15.76 |
0.07 |
0.08 |
0 |
0.11 |
0.14 |
0.16 |
0.19 |
0.22 |
0.26 |
0.31 |
13.96 |
19.96 |
15.92 |
15.61 |
0.07 |
0.08 |
0.1 |
0 |
0.14 |
0.16 |
0.19 |
0.22 |
0.26 |
0.31 |
18.05 |
16.86 |
18.78 |
17.9 |
0.07 |
0.08 |
0.1 |
0.11 |
0 |
0.16 |
0.19 |
0.22 |
0.26 |
0.31 |
14.36 |
18.67 |
16.81 |
16.62 |
0.07 |
0.08 |
0.1 |
0.11 |
0.14 |
0 |
0.19 |
0.22 |
0.26 |
0.31 |
15.91 |
17.52 |
15.76 |
16.4 |
0.07 |
0.08 |
0.1 |
0.11 |
0.14 |
0.16 |
0 |
0.22 |
0.26 |
0.31 |
17.08 |
17.47 |
17.48 |
17.34 |
0.07 |
0.08 |
0.1 |
0.11 |
0.14 |
0.16 |
0.19 |
0 |
0.26 |
0.31 |
14.34 |
17.91 |
17.73 |
16.66 |
0.07 |
0.08 |
0.1 |
0.11 |
0.14 |
0.16 |
0.19 |
0.22 |
0 |
0.31 |
18.35 |
15.92 |
16.2 |
16.82 |
0.07 |
0.08 |
0.1 |
0.11 |
0.14 |
0.16 |
0.19 |
0.22 |
0.26 |
0 |
17.23 |
16.01 |
16.92 |
16.72 |
0.07 |
0.08 |
0.1 |
0.11 |
0.14 |
0.16 |
0.19 |
0.22 |
0.26 |
0.31 |
14.85 |
14.32 |
15.39 |
17.86 |
The column labella “xi” contains the experimental levels of drug Ai, i = 1,…,10 |
|||||||||||||
x1 |
x2 |
x3 |
x4 |
x5 |
y1 |
y2 |
y3 |
y4 |
y5 |
y6 |
y7 |
y8 |
y |
0.01 |
0 |
0 |
0 |
0 |
78.45 |
77.61 |
80.25 |
79.01 |
78.46 |
79.32 |
80.11 |
80.11 |
79.17 |
0.02 |
0 |
0 |
0 |
0 |
68.03 |
69.42 |
69.36 |
67.21 |
69.51 |
69.3 |
70.69 |
69.52 |
69.13 |
0.04 |
0 |
0 |
0 |
0 |
59.13 |
58.56 |
58.73 |
58.4 |
59.99 |
58.78 |
59.43 |
58.61 |
58.95 |
0.07 |
0 |
0 |
0 |
0 |
48.11 |
49.44 |
48.06 |
50.15 |
49.63 |
48.31 |
51.28 |
50.1 |
49.39 |
0.14 |
0 |
0 |
0 |
0 |
39.67 |
40.03 |
39.85 |
39.64 |
41.42 |
40.01 |
39.85 |
38.31 |
39.85 |
0.27 |
0 |
0 |
0 |
0 |
29.28 |
28.94 |
30.66 |
28.73 |
29.24 |
28.5 |
28.61 |
30.09 |
29.26 |
0.51 |
0 |
0 |
0 |
0 |
22.18 |
19.71 |
19.7 |
19.37 |
19.26 |
19.97 |
17.8 |
20.81 |
19.72 |
0.99 |
0 |
0 |
0 |
0 |
11.29 |
10.5 |
9.61 |
10.4 |
8.4 |
11.48 |
9.82 |
10.36 |
10.23 |
0 |
0.01 |
0 |
0 |
0 |
81.58 |
82.24 |
83.77 |
83.09 |
84.99 |
83.66 |
84.79 |
84.96 |
83.63 |
0 |
0.02 |
0 |
0 |
0 |
74.67 |
75.27 |
73.13 |
75.21 |
75.1 |
74.09 |
74.55 |
76.27 |
74.79 |
0 |
0.04 |
0 |
0 |
0 |
62.99 |
66.81 |
63.89 |
63.74 |
64.3 |
65.28 |
64.8 |
65.31 |
64.64 |
0 |
0.07 |
0 |
0 |
0 |
54.28 |
55.5 |
54.36 |
56.35 |
55.44 |
54.24 |
53.96 |
54.81 |
54.87 |
0 |
0.14 |
0 |
0 |
0 |
44.86 |
44.38 |
44.74 |
43.61 |
44.88 |
45.72 |
44.84 |
45.33 |
44.79 |
0 |
0.27 |
0 |
0 |
0 |
35.59 |
35.27 |
34.78 |
35.04 |
35.14 |
34.5 |
33.21 |
35.27 |
34.85 |
0 |
0.51 |
0 |
0 |
0 |
24.73 |
23.96 |
25.61 |
23.48 |
25.11 |
26.01 |
24.24 |
23.68 |
24.6 |
0 |
0.99 |
0 |
0 |
0 |
16.73 |
17.03 |
15.26 |
14.43 |
15.59 |
15.78 |
14.33 |
14.73 |
15.49 |
0 |
0 |
0.01 |
0 |
0 |
88.6 |
90.02 |
90.89 |
88.48 |
89.18 |
88.87 |
89.6 |
90.3 |
89.49 |
0 |
0 |
0.02 |
0 |
0 |
79.56 |
80.02 |
79.54 |
79.63 |
82.02 |
78.37 |
79.22 |
79.19 |
79.69 |
0 |
0 |
0.04 |
0 |
0 |
70.05 |
68.51 |
71.19 |
70.33 |
68.22 |
68.34 |
68.23 |
69.97 |
69.35 |
0 |
0 |
0.07 |
0 |
0 |
59.62 |
59.86 |
58.81 |
59.84 |
57.68 |
59.27 |
59.53 |
58.53 |
59.14 |
0 |
0 |
0.14 |
0 |
0 |
50.57 |
49.13 |
50.22 |
49.32 |
48.55 |
49.25 |
49 |
49.76 |
49.48 |
0 |
0 |
0.27 |
0 |
0 |
40.17 |
39.53 |
39.58 |
40.66 |
38.75 |
39.44 |
39.18 |
40.44 |
39.72 |
0 |
0 |
0.51 |
0 |
0 |
29.21 |
29.43 |
30.6 |
30.8 |
29.56 |
30.98 |
30.86 |
28.64 |
30.01 |
0 |
0 |
0.99 |
0 |
0 |
18.35 |
19.13 |
20.75 |
20.27 |
19.98 |
19.85 |
20.26 |
20.5 |
19.89 |
0 |
0 |
0 |
0.01 |
0 |
95.94 |
93.17 |
91.89 |
94.65 |
93.86 |
95.22 |
94.48 |
93.89 |
94.14 |
0 |
0 |
0 |
0.02 |
0 |
83.63 |
84.02 |
82.9 |
84.64 |
84.77 |
83.7 |
85.11 |
83.29 |
84.01 |
0 |
0 |
0 |
0.04 |
0 |
74.49 |
72.68 |
72.94 |
73.4 |
74.77 |
75.36 |
74.56 |
74.35 |
74.07 |
0 |
0 |
0 |
0.07 |
0 |
65.1 |
65.14 |
64.94 |
65.3 |
65.29 |
64.01 |
65.09 |
62.64 |
64.69 |
0 |
0 |
0 |
0.14 |
0 |
54.8 |
54.57 |
56.16 |
54.03 |
56.47 |
54.87 |
55.37 |
52.56 |
54.85 |
0 |
0 |
0 |
0.27 |
0 |
43.94 |
45.54 |
44.52 |
44.24 |
46.07 |
45.81 |
46.01 |
43.67 |
44.97 |
0 |
0 |
0 |
0.51 |
0 |
34.53 |
35.27 |
35.81 |
35.17 |
33.71 |
34.58 |
35.47 |
34.01 |
34.82 |
0 |
0 |
0 |
0.99 |
0 |
25.03 |
25.64 |
25.7 |
24.84 |
22.82 |
24.71 |
26.56 |
23.98 |
24.91 |
0 |
0 |
0 |
0 |
0.01 |
100.56 |
97.59 |
98.03 |
98.95 |
99.98 |
101.08 |
99.1 |
97.35 |
99.08 |
0 |
0 |
0 |
0 |
0.02 |
88.37 |
88.21 |
89.63 |
89.83 |
87.4 |
90.18 |
89.18 |
89.52 |
89.04 |
0 |
0 |
0 |
0 |
0.04 |
80.17 |
78.94 |
78.63 |
80.43 |
79.45 |
78.95 |
81.09 |
77.79 |
79.43 |
0 |
0 |
0 |
0 |
0.07 |
69.85 |
69.65 |
71.05 |
69.34 |
69.57 |
70.19 |
69.03 |
69.65 |
69.79 |
0 |
0 |
0 |
0 |
0.14 |
59.46 |
60.82 |
59.66 |
60.02 |
61.92 |
59.33 |
59.69 |
60.48 |
60.17 |
0 |
0 |
0 |
0 |
0.27 |
48.79 |
49.55 |
51.48 |
49.61 |
49.77 |
50.55 |
50.76 |
49.84 |
50.04 |
0 |
0 |
0 |
0 |
0.51 |
39.71 |
41.26 |
39.57 |
40.23 |
39.49 |
41.41 |
40.15 |
40.09 |
40.24 |
0 |
0 |
0 |
0 |
0.99 |
30.06 |
30.63 |
30.74 |
30.59 |
30.39 |
28.55 |
31.56 |
29.77 |
30.29 |
The column labella “xi” contains the experimental levels of drug Ai, i = 1,…,5 |
|||||||||||||
x1 |
x2 |
x3 |
x4 |
x5 |
y1 |
y2 |
y3 |
y |
|||||
0.07 |
0 |
0.14 |
0 |
0.26 |
42.59 |
41.31 |
41.99 |
41.96 |
|||||
0 |
0.1 |
0.14 |
0.19 |
0 |
33.92 |
36.13 |
34.54 |
34.87 |
|||||
0 |
0.1 |
0.14 |
0 |
0.26 |
40.73 |
41.09 |
40.83 |
40.89 |
|||||
0 |
0.1 |
0 |
0.19 |
0.26 |
34.99 |
33.52 |
33.81 |
34.11 |
|||||
0.07 |
0.1 |
0.14 |
0.19 |
0 |
30.69 |
29.29 |
29.07 |
29.68 |
|||||
0.07 |
0.1 |
0.14 |
0 |
0.26 |
35.89 |
33.31 |
36.15 |
35.12 |
|||||
0.07 |
0.1 |
0 |
0.19 |
0.26 |
29.6 |
28.86 |
28.04 |
28.83 |
|||||
0.07 |
0 |
0.14 |
0.19 |
0.26 |
33.17 |
33.78 |
33.4 |
33.45 |
|||||
0 |
0.1 |
0.14 |
0.19 |
0.26 |
32.8 |
32.99 |
33.45 |
33.08 |
|||||
0.07 |
0.1 |
0.14 |
0.19 |
0.26 |
29.31 |
29.66 |
29.83 |
29.6 |
|||||
The column labella “xi” contains the experimental levels of drug Ai, i = 1,…,5 |
|||||||||||||
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
x8 |
x9 |
x10 |
y1 |
y2 |
y3 |
y4 |
y5 |
y6 |
y7 |
y8 |
y |
0.01 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
79.93 |
79.57 |
79.11 |
77.59 |
78.85 |
79.33 |
78.55 |
79.85 |
79.1 |
0.02 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
70.1 |
69.59 |
71.1 |
68.78 |
68.32 |
68.51 |
67.95 |
69.5 |
69.23 |
0.04 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
62.69 |
59.56 |
60.3 |
60.37 |
59.08 |
58.92 |
60.07 |
60.09 |
60.13 |
0.07 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
49.86 |
50.15 |
50.36 |
48.4 |
48.45 |
49.94 |
50.33 |
49.7 |
49.65 |
0.14 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
37.63 |
38.97 |
38.74 |
39.15 |
40.08 |
39.78 |
41.02 |
40.15 |
39.44 |
0.27 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
29.9 |
29.89 |
29.87 |
29.98 |
29.75 |
30.19 |
30.4 |
29.27 |
29.91 |
0.51 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
19.65 |
18.27 |
20.09 |
19.32 |
18.21 |
18.31 |
18.68 |
18.5 |
18.88 |
0.99 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
9.02 |
10.82 |
9.85 |
8.92 |
9.86 |
10.22 |
11.43 |
9.59 |
9.96 |
0 |
0.01 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
82.22 |
82.7 |
82.03 |
83.93 |
81.84 |
81.76 |
81.22 |
82.98 |
82.33 |
0 |
0.02 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
72.09 |
71.65 |
72.51 |
71.17 |
70.75 |
71.09 |
71.43 |
72.34 |
71.63 |
0 |
0.04 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
63.95 |
63.73 |
63.32 |
62.11 |
61.14 |
61.17 |
61.91 |
62.2 |
62.44 |
0 |
0.07 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
51.82 |
53.31 |
52.3 |
51.86 |
52 |
52.87 |
50.65 |
52.39 |
52.15 |
0 |
0.14 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
43.11 |
40.37 |
43.46 |
41.26 |
40.04 |
41.02 |
42.39 |
41.75 |
41.67 |
0 |
0.27 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
34.37 |
30.3 |
30.09 |
31.87 |
31.3 |
31.58 |
34.03 |
34.25 |
32.22 |
0 |
0.51 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
21.41 |
21.74 |
21.79 |
22.23 |
22.68 |
21.78 |
21.66 |
23.18 |
22.06 |
0 |
0.99 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
12.3 |
14.57 |
13.24 |
11.23 |
12.6 |
15.25 |
12.68 |
10.16 |
12.75 |
0 |
0 |
0.01 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
84.98 |
83.75 |
85.66 |
84.32 |
83.7 |
83.54 |
82.47 |
84.92 |
84.17 |
0 |
0 |
0.02 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
75.27 |
73.93 |
73.78 |
73.99 |
72.71 |
73.9 |
75.75 |
74.75 |
74.26 |
0 |
0 |
0.04 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
65.59 |
64.84 |
66.49 |
63.37 |
65.07 |
63.94 |
64.11 |
65.43 |
64.85 |
0 |
0 |
0.07 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
52.8 |
54.66 |
55.71 |
53.88 |
55.26 |
56.04 |
53.8 |
54.75 |
54.61 |
0 |
0 |
0.14 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
45.51 |
44.18 |
47.52 |
47.1 |
43.64 |
44.5 |
45.19 |
43.35 |
45.12 |
0 |
0 |
0.27 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
35.92 |
36.38 |
35.14 |
35.48 |
35.81 |
33.02 |
34.85 |
34.03 |
35.08 |
0 |
0 |
0.51 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
25.19 |
24.91 |
25.24 |
25.85 |
25.65 |
24.19 |
22.61 |
22.59 |
24.53 |
0 |
0 |
0.99 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
16.25 |
15.01 |
16.32 |
13.9 |
16.31 |
15 |
16.47 |
15.92 |
15.65 |
0 |
0 |
0 |
0.01 |
0 |
0 |
0 |
0 |
0 |
0 |
85.86 |
88.1 |
86.99 |
86.54 |
85.61 |
86.93 |
87.8 |
85.72 |
86.69 |
0 |
0 |
0 |
0.02 |
0 |
0 |
0 |
0 |
0 |
0 |
76.42 |
76.54 |
78.31 |
77.13 |
78.09 |
76.36 |
78.8 |
76.25 |
77.24 |
0 |
0 |
0 |
0.04 |
0 |
0 |
0 |
0 |
0 |
0 |
66.67 |
65.7 |
66.82 |
67.28 |
67.41 |
67.24 |
67.35 |
66.47 |
66.87 |
0 |
0 |
0 |
0.07 |
0 |
0 |
0 |
0 |
0 |
0 |
58.51 |
58.1 |
56.9 |
56.94 |
57.74 |
56.82 |
59.85 |
57.37 |
57.78 |
0 |
0 |
0 |
0.14 |
0 |
0 |
0 |
0 |
0 |
0 |
47.3 |
47.59 |
47.21 |
48.03 |
48.14 |
47.89 |
45.82 |
46.86 |
47.35 |
0 |
0 |
0 |
0.27 |
0 |
0 |
0 |
0 |
0 |
0 |
36.95 |
34.48 |
38.85 |
37.74 |
38.35 |
37.72 |
38.08 |
37.15 |
37.41 |
0 |
0 |
0 |
0.51 |
0 |
0 |
0 |
0 |
0 |
0 |
25.51 |
28.72 |
26.82 |
27.68 |
29.35 |
29.06 |
28.21 |
28.22 |
27.95 |
0 |
0 |
0 |
0.99 |
0 |
0 |
0 |
0 |
0 |
0 |
19.84 |
16.87 |
19.24 |
15.7 |
16.45 |
17.09 |
18.41 |
17.93 |
17.69 |
0 |
0 |
0 |
0 |
0.01 |
0 |
0 |
0 |
0 |
0 |
89.82 |
87.44 |
89.69 |
89.83 |
89.3 |
87.53 |
89.48 |
88.62 |
88.96 |
0 |
0 |
0 |
0 |
0.02 |
0 |
0 |
0 |
0 |
0 |
80.46 |
77.69 |
79.44 |
79.54 |
77.82 |
76.73 |
79.12 |
79.41 |
78.78 |
0 |
0 |
0 |
0 |
0.04 |
0 |
0 |
0 |
0 |
0 |
70.67 |
68.22 |
69.06 |
68.62 |
70.08 |
69.3 |
69.74 |
68.88 |
69.32 |
0 |
0 |
0 |
0 |
0.07 |
0 |
0 |
0 |
0 |
0 |
59.86 |
58.19 |
60.54 |
59.37 |
58.35 |
61.32 |
59.34 |
59.8 |
59.6 |
0 |
0 |
0 |
0 |
0.14 |
0 |
0 |
0 |
0 |
0 |
50.01 |
51.18 |
49.48 |
49.04 |
48.42 |
48.99 |
49.54 |
47.91 |
49.32 |
0 |
0 |
0 |
0 |
0.27 |
0 |
0 |
0 |
0 |
0 |
39.35 |
40.99 |
39.77 |
41.36 |
40.6 |
40.38 |
39.79 |
38.36 |
40.07 |
0 |
0 |
0 |
0 |
0.51 |
0 |
0 |
0 |
0 |
0 |
28.87 |
29.84 |
31.37 |
30.41 |
29.07 |
30.65 |
31.03 |
28.47 |
29.96 |
0 |
0 |
0 |
0 |
0.99 |
0 |
0 |
0 |
0 |
0 |
20.27 |
21.95 |
21.72 |
20.36 |
20.32 |
21.33 |
21.2 |
19.92 |
20.88 |
0 |
0 |
0 |
0 |
0 |
0.01 |
0 |
0 |
0 |
0 |
91.24 |
92.4 |
90.73 |
91.78 |
91.45 |
91.25 |
91.88 |
92.14 |
91.61 |
0 |
0 |
0 |
0 |
0 |
0.02 |
0 |
0 |
0 |
0 |
82.18 |
82.89 |
80.1 |
81.75 |
80.93 |
80.7 |
81.61 |
81.75 |
81.49 |
0 |
0 |
0 |
0 |
0 |
0.04 |
0 |
0 |
0 |
0 |
72.14 |
71.86 |
75.51 |
71.69 |
70.63 |
72.83 |
72.36 |
72.22 |
72.03 |
0 |
0 |
0 |
0 |
0 |
0.07 |
0 |
0 |
0 |
0 |
61.46 |
64.67 |
61.1 |
60.91 |
62.35 |
63.68 |
62.04 |
61.39 |
62.2 |
0 |
0 |
0 |
0 |
0 |
0.14 |
0 |
0 |
0 |
0 |
53.32 |
51.65 |
51.35 |
50.42 |
52.25 |
50.75 |
52.9 |
52.56 |
51.9 |
0 |
0 |
0 |
0 |
0 |
0.27 |
0 |
0 |
0 |
0 |
43.82 |
42.81 |
41.57 |
42.76 |
43.58 |
44.11 |
43.64 |
43.33 |
43.2 |
0 |
0 |
0 |
0 |
0 |
0.51 |
0 |
0 |
0 |
0 |
37.79 |
31.32 |
32.77 |
32.87 |
30.73 |
34.03 |
32.14 |
32.54 |
32.4 |
0 |
0 |
0 |
0 |
0 |
0.99 |
0 |
0 |
0 |
0 |
22.91 |
22.93 |
24.59 |
23.5 |
22.94 |
23.1 |
21.99 |
22.74 |
23.09 |
0 |
0 |
0 |
0 |
0 |
0 |
0.01 |
0 |
0 |
0 |
93.89 |
95.52 |
92.99 |
95.3 |
94.04 |
95.08 |
95.4 |
94.92 |
94.64 |
0 |
0 |
0 |
0 |
0 |
0 |
0.02 |
0 |
0 |
0 |
85.85 |
84.19 |
84.68 |
84.77 |
85.4 |
86.41 |
86.16 |
86.23 |
85.46 |
0 |
0 |
0 |
0 |
0 |
0 |
0.04 |
0 |
0 |
0 |
74.02 |
73.97 |
75.37 |
74.09 |
75.58 |
75.94 |
74.98 |
73.74 |
74.71 |
0 |
0 |
0 |
0 |
0 |
0 |
0.07 |
0 |
0 |
0 |
63.57 |
63.35 |
64.28 |
64.3 |
64.34 |
63.55 |
63.56 |
65 |
63.99 |
0 |
0 |
0 |
0 |
0 |
0 |
0.14 |
0 |
0 |
0 |
56.97 |
57.02 |
55.83 |
54.24 |
55.09 |
53.19 |
55.41 |
52.81 |
55.07 |
0 |
0 |
0 |
0 |
0 |
0 |
0.27 |
0 |
0 |
0 |
46.18 |
44.32 |
43.92 |
46.14 |
44.7 |
46.46 |
44.58 |
47.04 |
45.42 |
0 |
0 |
0 |
0 |
0 |
0 |
0.51 |
0 |
0 |
0 |
35.65 |
36.91 |
33.52 |
36.39 |
34.55 |
33.43 |
35.07 |
36.34 |
35.23 |
0 |
0 |
0 |
0 |
0 |
0 |
0.99 |
0 |
0 |
0 |
25.03 |
25.24 |
24.14 |
24.72 |
24.85 |
23.77 |
24.89 |
25.87 |
24.81 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0.01 |
0 |
0 |
94.83 |
98.18 |
96.96 |
96.8 |
96.58 |
97.13 |
96.15 |
96.85 |
96.69 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0.02 |
0 |
0 |
85.73 |
86.87 |
85.42 |
86.34 |
87.7 |
88.34 |
86.03 |
85.57 |
86.5 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0.04 |
0 |
0 |
76.92 |
77.21 |
76.88 |
76.81 |
77.96 |
77.18 |
77.56 |
77.03 |
77.19 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0.07 |
0 |
0 |
67.69 |
66.79 |
66.61 |
65.92 |
67.26 |
68.59 |
65.04 |
68.62 |
67.06 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0.14 |
0 |
0 |
55.8 |
57.95 |
57.7 |
55.96 |
56.54 |
56.63 |
56.17 |
58.22 |
56.87 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0.27 |
0 |
0 |
46.07 |
46.69 |
46.69 |
47.26 |
47.75 |
48.16 |
47.6 |
45.85 |
47.01 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0.51 |
0 |
0 |
38.1 |
38.13 |
37.62 |
37.21 |
37.86 |
36.94 |
37.73 |
39.15 |
37.84 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0.99 |
0 |
0 |
28.42 |
28.13 |
29.13 |
26.73 |
26.32 |
28.09 |
27.56 |
28.69 |
27.88 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0.01 |
0 |
99.39 |
99.88 |
97.62 |
99.92 |
98.57 |
99.13 |
97.71 |
97.75 |
98.75 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0.02 |
0 |
87.46 |
88.61 |
89.35 |
88.75 |
88.64 |
90.83 |
89.77 |
88.46 |
88.98 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0.04 |
0 |
79.4 |
77.52 |
79.73 |
79.91 |
77.28 |
79.2 |
77.38 |
78.33 |
78.59 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0.07 |
0 |
69.68 |
67.35 |
70.43 |
68.31 |
70.65 |
71.84 |
69.28 |
70.3 |
69.73 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0.14 |
0 |
60.82 |
62.4 |
59.03 |
60.58 |
61.74 |
59.15 |
58.79 |
59.7 |
60.28 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0.27 |
0 |
50.07 |
49.72 |
49.68 |
49.3 |
48.33 |
49.26 |
50.76 |
50.61 |
49.72 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0.51 |
0 |
38.82 |
39.72 |
39.65 |
40.69 |
40.86 |
38.02 |
40.47 |
37.27 |
39.44 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0.99 |
0 |
32.25 |
28.69 |
29.77 |
30.9 |
28.71 |
28.85 |
30.63 |
30.12 |
29.99 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0.01 |
99.93 |
99.05 |
98.46 |
98.82 |
99.04 |
99.7 |
99.42 |
99.91 |
99.42 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0.02 |
91.42 |
93.51 |
92.25 |
91.98 |
92.08 |
93.02 |
90.88 |
90.69 |
91.98 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0.04 |
80.96 |
81.84 |
79.8 |
81.46 |
82.55 |
82.83 |
81.22 |
82.88 |
81.69 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0.07 |
72.57 |
73.04 |
72.16 |
72.39 |
71.72 |
73.05 |
73.64 |
72.09 |
72.58 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0.14 |
63.25 |
61.1 |
61.81 |
61.46 |
61.5 |
61.78 |
61.41 |
63.37 |
61.96 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0.27 |
52.18 |
52.59 |
52.15 |
51.64 |
49.94 |
54.16 |
50.94 |
54.12 |
52.22 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0.51 |
42.29 |
41.76 |
39.96 |
43.25 |
43.25 |
41.3 |
42.22 |
40.76 |
41.71 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0.99 |
32.08 |
31.6 |
33.03 |
32.46 |
32.46 |
32.35 |
32.51 |
34.23 |
32.53 |
The column labella “xi” contains the experimental levels of drug Ai, i = 1,…,10 |
||||||||||||||||||
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
x8 |
x9 |
x10 |
y1 |
y2 |
y3 |
y |
0 |
0.08 |
0.1 |
0.11 |
0.14 |
0 |
0.19 |
0.22 |
0.26 |
0.31 |
19.5 |
19.06 |
18.55 |
19.04 |
0.07 |
0 |
0.1 |
0.11 |
0.14 |
0.16 |
0.19 |
0.22 |
0.26 |
0 |
18.25 |
18.59 |
19.19 |
18.68 |
0.07 |
0.08 |
0.1 |
0 |
0.14 |
0.16 |
0 |
0.22 |
0.26 |
0.31 |
18.19 |
19.23 |
17.7 |
18.37 |
0.07 |
0.08 |
0 |
0.11 |
0 |
0.16 |
0.19 |
0.22 |
0.26 |
0.31 |
16.96 |
19.66 |
17.71 |
18.11 |
0.07 |
0.08 |
0.1 |
0 |
0.14 |
0.16 |
0.19 |
0.22 |
0 |
0.31 |
18.15 |
20.58 |
18.14 |
18.96 |
0 |
0.08 |
0.1 |
0.11 |
0.14 |
0.16 |
0.19 |
0 |
0.26 |
0.31 |
18.53 |
17.99 |
16.56 |
17.69 |
0.07 |
0.08 |
0 |
0.11 |
0.14 |
0 |
0.19 |
0.22 |
0.26 |
0.31 |
17.18 |
17.37 |
18.04 |
17.53 |
0.07 |
0 |
0.1 |
0.11 |
0.14 |
0.16 |
0.19 |
0.22 |
0 |
0.31 |
18.94 |
17.09 |
18.37 |
18.13 |
0.07 |
0.08 |
0.1 |
0.11 |
0 |
0.16 |
0.19 |
0.22 |
0.26 |
0 |
18.33 |
18.3 |
16.99 |
17.87 |
0 |
0.08 |
0.1 |
0.11 |
0.14 |
0.16 |
0.19 |
0.22 |
0.26 |
0.31 |
16.39 |
16.11 |
16.27 |
16.26 |
0.07 |
0 |
0.1 |
0.11 |
0.14 |
0.16 |
0.19 |
0.22 |
0.26 |
0.31 |
14.33 |
16.71 |
16.24 |
15.76 |
0.07 |
0.08 |
0 |
0.11 |
0.14 |
0.16 |
0.19 |
0.22 |
0.26 |
0.31 |
13.96 |
19.96 |
15.92 |
15.61 |
0.07 |
0.08 |
0.1 |
0 |
0.14 |
0.16 |
0.19 |
0.22 |
0.26 |
0.31 |
18.05 |
16.86 |
18.78 |
17.9 |
0.07 |
0.08 |
0.1 |
0.11 |
0 |
0.16 |
0.19 |
0.22 |
0.26 |
0.31 |
14.36 |
18.67 |
16.81 |
16.62 |
0.07 |
0.08 |
0.1 |
0.11 |
0.14 |
0 |
0.19 |
0.22 |
0.26 |
0.31 |
15.91 |
17.52 |
15.76 |
16.4 |
0.07 |
0.08 |
0.1 |
0.11 |
0.14 |
0.16 |
0 |
0.22 |
0.26 |
0.31 |
17.08 |
17.47 |
17.48 |
17.34 |
0.07 |
0.08 |
0.1 |
0.11 |
0.14 |
0.16 |
0.19 |
0 |
0.26 |
0.31 |
14.34 |
17.91 |
17.73 |
16.66 |
0.07 |
0.08 |
0.1 |
0.11 |
0.14 |
0.16 |
0.19 |
0.22 |
0 |
0.31 |
18.35 |
15.92 |
16.2 |
16.82 |
0.07 |
0.08 |
0.1 |
0.11 |
0.14 |
0.16 |
0.19 |
0.22 |
0.26 |
0 |
17.23 |
16.01 |
16.92 |
16.72 |
0.07 |
0.08 |
0.1 |
0.11 |
0.14 |
0.16 |
0.19 |
0.22 |
0.26 |
0.31 |
14.85 |
14.32 |
15.39 |
17.86 |
The column labella “xi” contains the experimental levels of drug Ai, i = 1,…,10 |
|||||||||||||






































