Top Links
Journal of Antibiotics Research
ISSN: 2574-5980
Analysis of Antibody by Real-Valued Special Functions
Copyright: © 2018 Zhao B. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Related article at Pubmed, Google Scholar
Background: Along with the rapid development of genetic engineering technology and antibody engineering technology, humanized monoclonal antibody has been rapidly developed and gradually replaces the rat sourced monoclonal antibody. In this paper, we establish two new logarithmically completely monotonic functions involving the real-valued special functions according to two preferred interaction geometries, necessary and sufficient conditions are presented for one of them to be logarithmically completely monotonic. As a consequence, a sharp inequality involving the real-valued special functions is deduced to solve the problems of genetically engineered antibody.
Keywords: Real-valued Special Functions; Genetically Engineered Antibody; Logarithmically Completely Monotonic; Inequality; Psi function
Antibodies have been proven to be indispensable tools for biomedical applications. Different engineered antibodies have been developed for various purposes according to the amino acid sequence and/or spatial structure of protein (Figure 1). At present, it is still difficult to predict the optimal structure of antibodies. Topology knowledge can be important in antibody application as well as transformation. Theoretically, we can obtain desired antibodies by using protein/gene engineering technology. For instance, we can transform the complementarity determining region (CDR) to promote the affinity of the antibody to antigen. Similarly, we could also transform any domain of antibody to make it bind with any desired target. Under this vision, topology is a powerful tool to predict the structure of protein and it will serve to antibody engineering. Our present work tries to explain, and predict, if possible, the change of structure, size and function of antibodies as well as their fragments from a topological perspective.
For 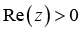 the classical Euler’s gamma function
the classical Euler’s gamma function ![]() and psi (digamma) function
and psi (digamma) function ![]() are defined by
are defined by
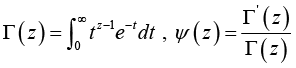 (1.1)
(1.1)respectively. The derivatives ![]() for
for ![]() are known as polygamma functions. For
are known as polygamma functions. For ![]() [1], the following series representations are established :
[1], the following series representations are established :
where 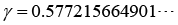 denotes the Euler’s constant.
denotes the Euler’s constant.
We next recall that a function f is said to be completely monotonic on an interval I , if f has derivatives of all orders on I which alternate successively in sign, that is,
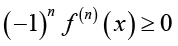 (1.5)
(1.5)for all ![]() and for all
and for all ![]() . If inequality (1.5) is strict for all
. If inequality (1.5) is strict for all ![]() and all
and all ![]() , then f is said to be strictly completely monotonic [2-5].
, then f is said to be strictly completely monotonic [2-5].
The classical Bernstein–Widder theorem [6, p. 160, Theorem 12a] states that a function f is completely monotonic on ![]() if and only if it is a Laplace transform of some nonnegative measure
if and only if it is a Laplace transform of some nonnegative measure ![]() , that is,
, that is,
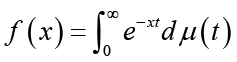 (1.6)
(1.6)where ![]() is non-decreasing and the integral converges for x >0 .
is non-decreasing and the integral converges for x >0 .
We recall also that a positive function f is said to be logarithmically completely monotonic on an interval I if f has derivatives of all orders on I and
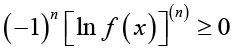 (1.7)
(1.7)for all ![]() and for all
and for all ![]() . If inequality (1.7) is strict for all
. If inequality (1.7) is strict for all ![]() and all
and all ![]() , then f is said to be strictly logarithmically completely monotonic [7-9].
, then f is said to be strictly logarithmically completely monotonic [7-9].
The antibody structure will be changed when it binds certain targets (Figure 2a), i.e.: antigen, receptor. How to describe the changes in the view of topology? The following cases will explain it in detail.
It was proved explicitly in and other articles that a logarithmically completely monotonic function must be completely monotonic [8]. In [10], G. D. Anderson et al. proved that the function
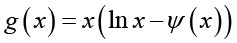 (1.8)
(1.8)is strictly decreasing and strictly convex on ![]() , with two limits
, with two limits
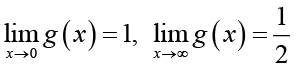 (1.9)
(1.9)From (1.9) and the monotonicity of g(x), then the double inequalities
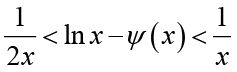 (1.10)
(1.10)holds for all x >0.
In [11, Theorem 1], by using the well-known Binet’s formula, H. Alzer generalized the monotonicity and convexity of g(x), that is, the function
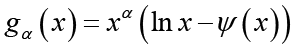 (1.11)
(1.11)is strictly completely monotonic on ![]() if and only if
if and only if ![]() .
.
In [12], D. Kershaw and A. Laforgia proved that the function 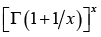 is decreasing on
is decreasing on ![]() and
and 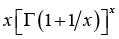 is increasing on
is increasing on ![]() . These are equivalent to the function
. These are equivalent to the function 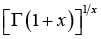 being increasing and
being increasing and 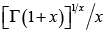 being decreasing on
being decreasing on ![]() , respectively.
, respectively.
In [13,Theorem 5], F. Qi and Ch.-p. Chen generalized these functions. They obtained the fact that for all x>0 the function 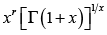 is strictly increasing for
is strictly increasing for ![]() and strictly decreasing for
and strictly decreasing for ![]() , respectively.
, respectively.
After the papain digestion, the remained antibody functional part (usually the Fab domain), will be smaller and the structure is also changed (Figure 1b). These changes can be revealed vividly using topology. Recently [14,Theorem 1], F. Qi, C.-F Wei and B.-N Guo established another excellent result, which states that for given 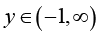 and
and  , let
, let
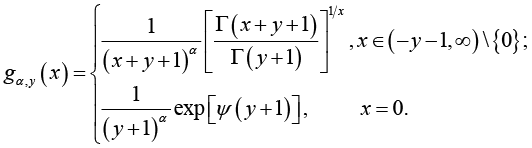 (1.12)
(1.12)The function (1.12) is logarithmically completely monotonic with respect to  if and only if
if and only if  ; and if
; and if 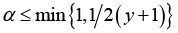 , the reciprocal of the function (1.12) is logarithmically completely monotonic with respect to
, the reciprocal of the function (1.12) is logarithmically completely monotonic with respect to 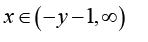
Antibodies occur spontaneously gathering and forming dimer, polymer, which will influence their functions (Figure 2b). In antibody engineering practice, it urgently needs some measures to overcome this difficulty. From topology perspective, we could understand this issue as follow.
Stimulated by the above results, we put forward the function as follows: for given 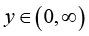 and real number
and real number ![]() , let the function
, let the function ![]() be defined by
be defined by
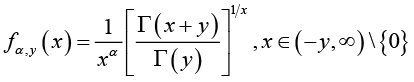 (1.13)
(1.13)Our first result is contained in the following theorem.
Theorem 1: For the function (1.13), then the following statements are true:
1) for any given ![]() , the function (1.13) is strictly logarithmically completely monotonic with respect to
, the function (1.13) is strictly logarithmically completely monotonic with respect to 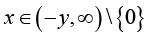 if and only if
if and only if ![]() ;
;
(2)for any given 0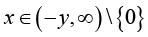 ;
;
(3) for any given y>0, the reciprocal of the function (1.13) is strictly logarithmically completely monotonic with respect to 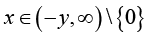 if and only if
if and only if ![]() .
.
Our second result is presented in the following theorem.
Theorem 2: For any given 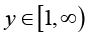 , let the function
, let the function ![]() be defined on
be defined on ![]() by
by
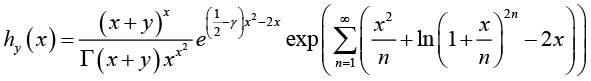 (1.14)
(1.14)where ![]() denotes the Euler’s constant, then the function (1.14) is strictly logarithmically completely monotonic with respect to x on
denotes the Euler’s constant, then the function (1.14) is strictly logarithmically completely monotonic with respect to x on ![]() .
.
The following corollary can be derived from Theorems 2 immediately.
Corollary 1: For any given ![]() , the inequality
, the inequality
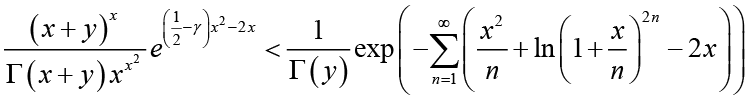 (1.15)
(1.15)holds for all x>0.
In order to prove our main results, we need the following lemmas.
It is well known that Bernoulli polynomials ![]() and Euler polynomials
and Euler polynomials ![]() are defined by
are defined by
Respectively [15]. The Bernoulli numbers Bn are denoted by Bn= Bn(0), while the Euler numbers En are defined by En = 2nEn(1/2).
In [16], the following summation formula is given:
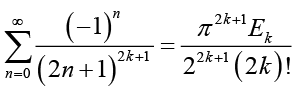 (2.3)
(2.3)for any nonnegative integer k, which implies
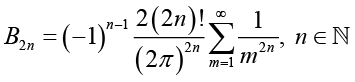 (2.4)
(2.4)In particular, it is known that for all
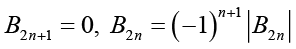 (2.5)
(2.5)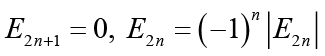 (2.6)
(2.6)And the first few nonzero values are
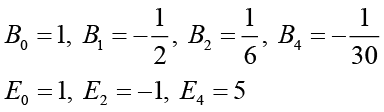
The Bernoulli and Euler numbers and polynomials are generalized ([18-21]).
(see [17, p.804, Chapter23]).
Lemma 1: For real number x > 0 and natural number m[22,23], then
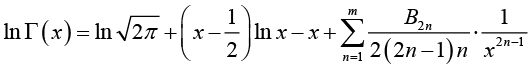 (2.7)
(2.7)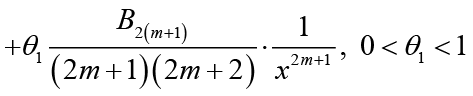
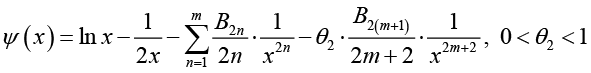 (2.8)
(2.8)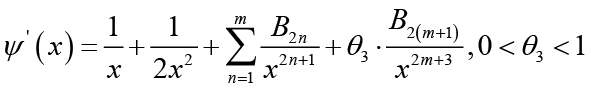 (2.9)
(2.9) (2.10)
(2.10)Remark 1: 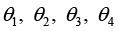 only depend on natural number m.
only depend on natural number m.
Lemma 2: For real number x > 0 and natural number ([24, p. 107, Lemma 3]),
we have
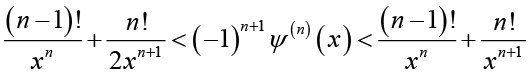 (2.11)
(2.11)Lemma 3: (see [1,17]) For real number x > 0 and natural number , we have
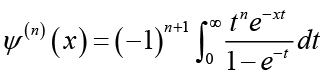 (2.14)
(2.14)Lemma 4: Let the sequence of functions for ![]() for
for ![]() be defined on
be defined on ![]() by
by
 (2.15)
(2.15)the series 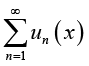 is differentiable on
is differentiable on ![]() , that is,
, that is,
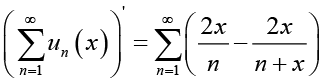 (2.16)
(2.16)Proof: It is obvious that 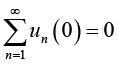 , therefore
, therefore 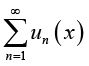 converges at x=0. In order to prove (2.16), we need only to show that,
converges at x=0. In order to prove (2.16), we need only to show that,
the inner closed uniform convergence of the series 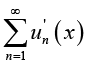 on
on ![]() . From (2.15), we have
. From (2.15), we have
 (2.17)
(2.17)For any interval
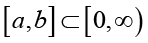 , we have
, we have
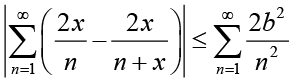 (2.18)
(2.18)for all 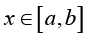 . It is easy to check that the series
. It is easy to check that the series ![]() converges, which and
converges, which and
Weierstrass M-test implies that the series 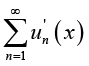 is inner closed uniformly convergent on
is inner closed uniformly convergent on 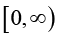 .
.
Hence the series 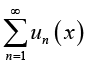 is differentiable on
is differentiable on 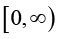 and the identity (2.17) holds for
and the identity (2.17) holds for 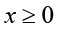 .
.
The lemma is proved.
Lemma 5: For 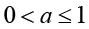 and real number b, let the function
and real number b, let the function 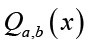 be defined by
be defined by
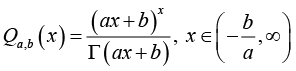 (2.19)
(2.19)If
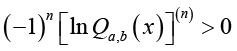 (2.20)
(2.20)for all ,
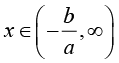 and n=2,3,---.
and n=2,3,---.
: Taking the logarithm of 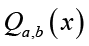 yields
yields
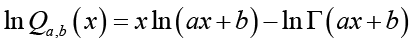 (2.21)
(2.21)and differentiating
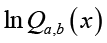 , then
, then
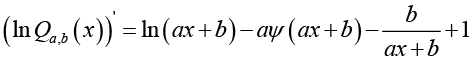 (2.22)
(2.22)For given integer ![]() , we get
, we get
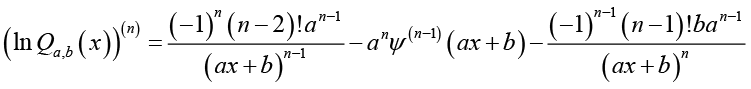 (2.23)
(2.23)and, by the identities (2.13) and (2.14), (2.23) can be written as
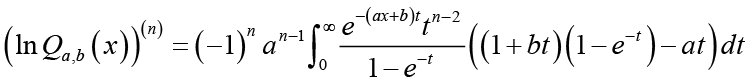 (2.24)
(2.24)Let 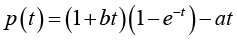 and
and 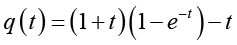 . It is easy to check that
. It is easy to check that
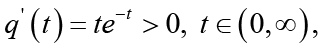 (2.25)
(2.25)therefore q(t) is strictly increasing on ![]() , and then
, and then 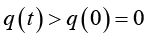 .
.
The following two cases will complete the proof of Lemma 5.
Case 1: If 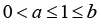 , then since q(t) > 0 for t > 0, we have
, then since q(t) > 0 for t > 0, we have
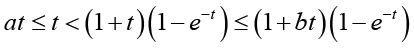 (2.26)
(2.26)which implies 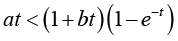 , and then p(t) > 0 for all t > 0.
, and then p(t) > 0 for all t > 0.
Case 2: If 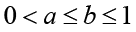 , then we get
, then we get
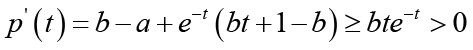
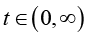 (2.27)
(2.27)therefore p(t) is strictly increasing on
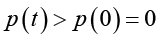 .
.
From (2.24), we know that the inequality (2.20) holds for 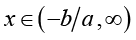 and integer .
The lemma is proved.
and integer .
The lemma is proved.
Proof of Theorem 1: For ![]() and natural number n, taking the logarithmically
and natural number n, taking the logarithmically
differential into consideration yields
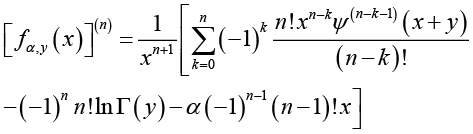 (3.1)
(3.1)where 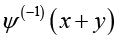 and
and 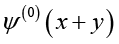 stand for
stand for 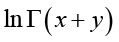 and
and 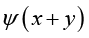 respectively.
respectively.
Furthermore, differentiating 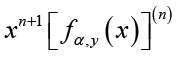 directly gives
directly gives
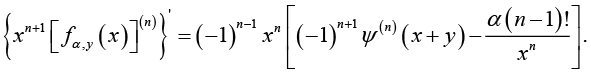 (3.2)
(3.2)Making use of (2.11) and (2.13) shows that for all
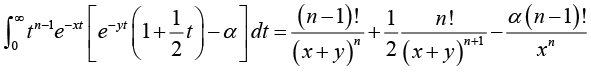
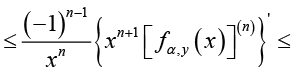 (3.3)
(3.3)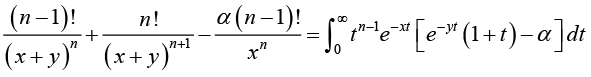
holds for all
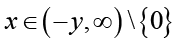 and
and 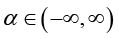 .
.
For any fixed 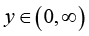 , let u(t) and v(t) be defined on
, let u(t) and v(t) be defined on 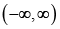 by
by
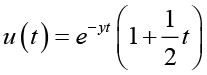
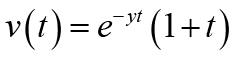
respectively.
Differentiating u(t) and v(t) directly, we obtain
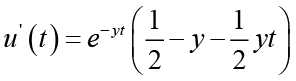 (3.4)
(3.4)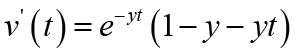 (3.5)
(3.5)Therefore, for given ![]() we have
we have
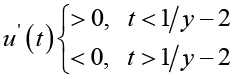 (3.6)
(3.6)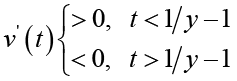 (3.7)
(3.7)From (3.6) and (3.7), we conclude that for all t > 0 we obtain
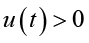
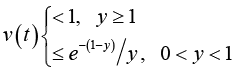 (3.9)
(3.9)From (3.3) and (3.8)-(3.9), it is easy to see that
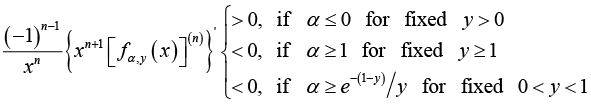 (3.10)
(3.10)for all
 .
.
On the one hand, if  , then the inequalities (3.10) can be equivalently
changed into
, then the inequalities (3.10) can be equivalently
changed into
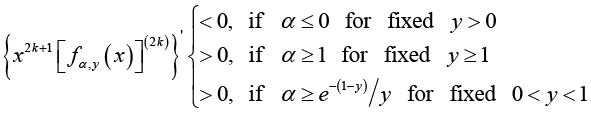 (3.11)
(3.11)and
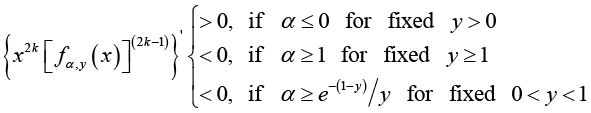 (3.12)
(3.12)for
From (3.1), then simple computation shows that
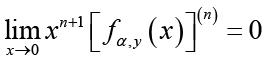 (3.13)
(3.13)for all
 . As a result,
. As a result,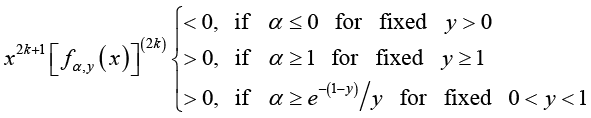 (3.14)
(3.14)and
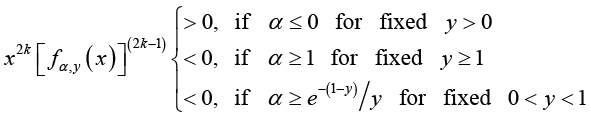 (3.15)
(3.15)for all
Therefore, (3.14) and (3.15) imply
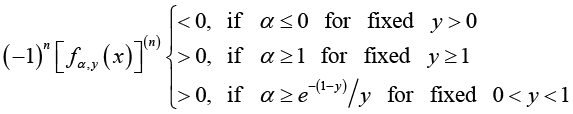 (3.16)
(3.16)for all
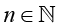
Hence, if either 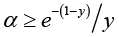 for given 0 < y < 1 or for given
for given 0 < y < 1 or for given ![]() , the function (1.13) is strictly logarithmically completely monotonic with respect to x on
, the function (1.13) is strictly logarithmically completely monotonic with respect to x on
![]() , and if
, and if ![]() for given y > 0, so is the reciprocal of the function (1.13).
for given y > 0, so is the reciprocal of the function (1.13).
On the other hand, if 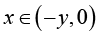 for any given y > 0, then (3.10) implies
for any given y > 0, then (3.10) implies
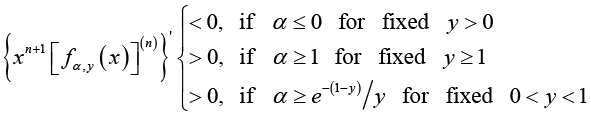 (3.17)
(3.17)for all
In view of (3.13), we can conclude that
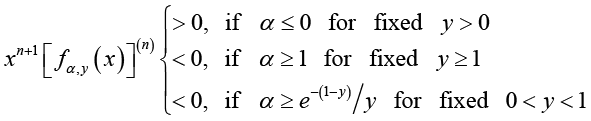 (3.18)
(3.18)for
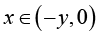 . Therefore, it is easy to prove similarly that (3.16) is also valid on
. Therefore, it is easy to prove similarly that (3.16) is also valid on 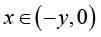 for any given y > 0 and all
for any given y > 0 and all The amino acid of antibody/protein possesses different preferences. Thus we can conduct site-directed mutation to promote the affinity and/or hydrophilic with the prediction of topology. For example, bovine antibodies have an unusual structure comprising a β-strand ‘stalk’ domain and a disulphide-bonded ‘knob’ domain in CDR3 (Figure 3). Attempts have been made to utilize such amino acid preference for antibody drug development.
Consequently, the function (1.13) is the same logarithmically completely monotonicity on (-y, 0) as on ![]() , that is, if either
, that is, if either 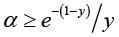 for given 0 < y < 1 or
for given 0 < y < 1 or ![]() for given
for given ![]() , the function (1.13) is strictly logarithmically completely monotonic with respect to x on (-y, 0), and if
, the function (1.13) is strictly logarithmically completely monotonic with respect to x on (-y, 0), and if ![]() for given y > 0, so is the reciprocal of the function (1.13).
for given y > 0, so is the reciprocal of the function (1.13).
Conversely, we assume that the reciprocal of the function (1.13) is strictly logarithmically completely monotonic on 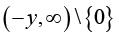 for any given y > 0. Then we have for any given y > 0 and all x > 0
for any given y > 0. Then we have for any given y > 0 and all x > 0
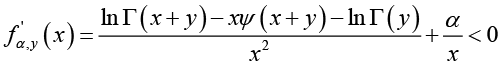 (3.19)
(3.19)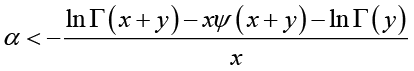 (3.20)
(3.20)By L’Hˆospital’s rule, we have
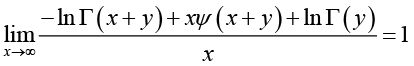 (3.21)
(3.21)for any given y > 0. By virtue of (3.20) and (3.21), we conclude that the necessary condition for the reciprocal of the function (1.13) to be strictly logarithmically completely monotonic is
If the function (1.13) is logarithmically completely monotonic on 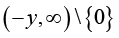
for any given y > 0, then the inequality (3.19) and (3.20) are reversed for any given y > 0 and all x > 0.
By utilizing (2.7) and (2.8), it is easy to see that
for any given y > 0. In fact, it is not difficult to show that the necessary condition for the function (1.13) to be strictly logarithmically completely monotonic is
The proof of Theorem 1 is completed.
Proof of Theorem 2: Taking the logarithm of ![]() gives
gives
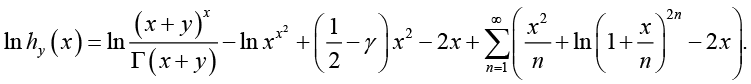 (3.23)
(3.23)Let
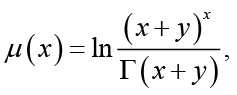 (3.24)
(3.24)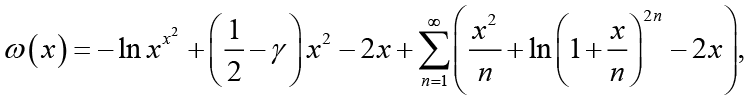 (3.25)
(3.25)then
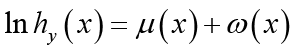 (3.26)
(3.26)In view of Lemma 4, straightforward calculation gives
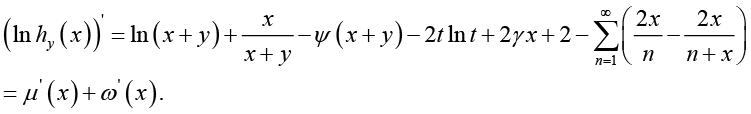 (3.27)
(3.27)By virtue of (1.2), the identity (3.27) is equivalent to
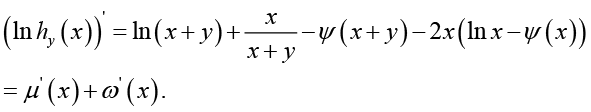 (3.28)
(3.28)By Lemma 5, we know that ![]() is strictly increasing on
is strictly increasing on ![]() , which and (1.10) imply the limit of
, which and (1.10) imply the limit of ![]() equals 1 as
equals 1 as  , therefore
, therefore
holds for all x > 0.
We know that g(x) is strictly completely monotonic on ![]() , where g(x) is defined by (1.8), hence for given integer
, where g(x) is defined by (1.8), hence for given integer ![]() , the inequality
, the inequality
holds for all x > 0.
And then by using inequality (1.9) and (1.10), we getReferences
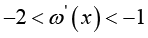 (3.31)
(3.31)for all x > 0.
From (3.29) and (3.31), we conclude that
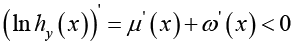 (3.32)
(3.32)for all x > 0. Utilizing Lemma 5 and (3.30), for given integer
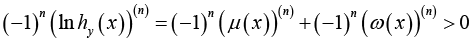 (3.33)
(3.33)for all x > 0.
Theorem 2 follows from (3.32) and (3.33).
Thus the proof of Theorem 2 is completed.
In conclusion, we establish two new logarithmically completely monotonic functions involving the real-valued special functions according to two preferred interaction geometries, and a sharp inequality involving the real-valued special functions is deduced to solve the problems of genetically engineering antibodies. It is necessary to address, many other aspects (such as thermal condition, alkalinity or acidity, adhesion of antibodies) are also playing key roles in antibodies functioning, which could be also understood from bio-mathematical perspective, and such knowledge will be in return useful for biomedical application of antibodies as well as proteins [25-30].
We would like to express my gratitude to all those who helped us during the writing of this article.
Figure 1: Different antibody formats. a: different antibody or engineered antibodies; b: different shape of antibody |
Figure 2: Model of pH-dependent conformational change of FcRY and structures for the FcRY monomer and dimer. a: FcRY has an extended conformation at pH 8 (s*= 7.2 S) with no predicted interaction between the CysR-FNII domains and the CTLDs. At pH 6 the CysR-FNII region folds back and binds to the CTLDs, resulting in a more compact conformation (s*= 7.9 S) that is able to bind IgY. b: Likely orientations of FcRY and FcRY–IgY on a membrane. The two FcRY monomers on the Right are shown in an orientation that would allow formation of a 2:1 FcRY–IgY complex |
Figure 3: Unique Structural Domain in Bovine IgG antibodies and application |






































