Top Links
Journal of Forensic Science & Criminology
ISSN: 2348-9804
Programming Scripts for Simple and Complex Paternity Testing based on Open-Source Programming Language from the R Project
Copyright: © 2014 Masataka Takamiya. This is an open-access article distributed under the terms of the Creative Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Related article at Pubmed, Google Scholar
Programming scripts were written for the statistical analysis of genetic data from simple cases and complex cases of undetermined paternity. The methods presented here involve algorithms constructed with R, an open-source and increasingly popular programming language used for calculations and statistics; these methods also involve conditional probability analysis, Bayes’ Theorem, and pedigree analysis. Previous computer programs for assessing probable paternity in complex cases of undetermined paternity have been written; however, only minimal or generalized formulas are described in the papers presenting these programs. Therefore, these previously published programs are difficult to understand for most forensic researchers. Here, we present the details of the calculations used to evaluate probabilities of paternity and the details of the R scripts used execute these calculations. These scripts were constructed not only for standard trio case where DNA typing of the mother, child, and the alleged father are available, but also for more complex cases where DNA typing of the alleged father is absent. In these more complex cases, the putative genotype of the alleged father is determined from the genotypes of his parents, his siblings, his wife, children known to be his biological children, or some combination of these people. This report provides concrete and orderly descriptions of the calculations and the R scripts so that each facet of this method is easily understood. Furthermore, access to these scripts will enable individual researchers to develop calculation systems of their own.
Keywords: Forensic mathematics; Paternity testing; R; DNA typing
DNA profiling is a powerful technique for paternity determinations [1]. Mathematical formulas for evaluating the plausibility of paternity of an individual have been developed based on Bayes’ Theorem [2-9]. Most cases of questioned paternity involve assessing the genotypes of a standard trio of individuals: the mother, the child, and an alleged father. However, a case is more complicated when the genotype of the alleged father is not available, but the genotype of one or more of the following individuals is available: his mother, his father, one or more of his siblings, his wife, or one or more of his biological children. Computer programs have been written for the purpose of determining paternity given genetic data from a complicated or incomplete pedigree [10-22]. However, most papers describing such programs provide only minimal and generalized calculations and are, therefore, accessible only to mathematicians and researchers with an excellent mathematical background. In other words, most forensic researchers are unfamiliar with the fundamental calculations used to assess these complicated pedigrees.
R is an increasingly popular and important programming language used for executing calculations and statistical analyses. R is an open-source tool that is distributed free of charge by the R project for statistical computing [23]. Therefore, R is being used by a growing number of researchers in bioinformatics and biostatistics. The merits of R for mathematical analyses have been described previously [24,25]. No extensive programming skills are required to exploit advantages of R, and it is easy to modify programs written in R. In other words, R enables an individual researcher to construct calculation systems tailored to their specific purpose. Since its facility and extensibility supersede those of other programs, R is becoming the standard system used for calculations and statistics. In addition, many educational facilities use R programs and R programming in mathematics and statistics courses [26]. Therefore, we believe that manipulation of R will become an essential skill for forensic researchers, and R is a promising tool for calculating the likelihood of paternity and a paternity index. Moreover, every calculation necessary for resolving a paternity case involving complex pedigrees can be clearly articulated in R scripts. The aims of this study were to develop R scripts for paternity determination for cases with or without DNA genotype data for the alleged father and to show the detailed and orderly calculations necessary for assessing complex pedigrees in paternity cases. This paper is intended to be both practical and highly educational.
To determine paternity in cases with or those without DNA typing information for the alleged father, computer programs were constructed based on conditional probability, Bayes’ Theorem, and pedigree analysis approaches. Each program relies on autosomal markers at a single locus, and is constructed on the assumption that all DNA-based genotyping is correct. They were built in R [23], and the calculations were based on formulas developed by Aoki et al. [11]. The contents of each script are shown in Table 1, and generalized pedigrees trees are presented in Figure 1 through 3.
Paternity Test Cases 1 and 2 are the standard trio case and duo case, respectively. Paternity Test Cases 3 through 8 are cases where DNA typing of the alleged father is not available, and his probable genotype was constructed based on DNA typing from one or some combination of the following individuals: his mother, his father, one or more of his siblings, his wife, one or more of his biological children. Thereafter, the probability of paternity was calculated for the alleged father (Figure 3B). In cases where DNA typing of the alleged father is available, Paternity Test Cases 1 and 2 are applicable. In contrast, it is necessary to use Paternity Test Cases 3 through 8, for cases where DNA types of the alleged father are not available. Furthermore, collecting genotypes from as many of the above-mentioned relatives would improve the ascertainment accuracy for Paternity Test Cases 3 through 8.
Paternity Test Case 3 (which includes six distinct scenarios) utilized genotypes of ascendants or descendants; Paternity Test Cases 4 through 8 utilized genotypes from combinations of ascendants and descendants. Some calculations imposed too heavy a burden for most computational systems; therefore, the required reductions in the number of calculations were made. Each program may deal with a maximum of 5 siblings, 5 biological children, or both. Relatives and genotypes were classified as shown in Figure 4 and Table 2 and Table 3. In each analysis, relatives of the alleged father were classified as either ascendants or decedents. DNA typing data of any one or any combination of these relatives could be used to construct a putative genotype for the alleged father. The ascendants category included the following individuals in the following groupings: 1) both of the alleged father’s parents; 2) one of his parents; 3) one of his parents and one or more of his siblings; and 4) one or more of his siblings. The descendants category included: 5) his wife and his biological children and (6) his biological children (Figure 4). In order to construct the probable genotype of an individual for whom DNA typing was not available, genotypes of the known biological children of that individual and the genotype of the other parent of those children were classified into 5 patterns (Table 2); similarly, the genotypes of the biological children of two such individuals (parents) were classified into 9 patterns to estimate the genotypes of both parents (Table 3). The number of scripts in each paternity test case, which are outside of broken lines in Figure 4, comes from the 5 patterns in Table 2 or 9 patterns in Table 3. In Paternity Test Cases 4 through 8, the scripts are basically constructed in combination with the classifications in Table 2 and Table 3. The numbers of the scripts in each paternity test case that are indicated inside of the broken line were derived from multiplications of these classifications. For example, Paternity Test Case 4 3 (n=25) was constructed based on a combination of Paternity Test Case 3 3 (n=5) and Paternity Test Case 3 5 (n=5).
For each program, we describe 1) the mathematical theory, and 2) the R scripts used for the calculations. R scripts in this section are described in pseudo-codes, so that they are easily understood. For Paternity Test Cases 3 through 8, only the calculations necessary for step 1 of the general rule shown in Figure 3 are listed in detail because the calculations necessary for step 2 in Paternity Test Cases 3 through 8 are fully explained in the description of Paternity Test Case 1. The general rule (Figure 3B) was only used for Paternity Test Cases 3 through 8; however, the only difference between step 2 of this general rule and the calculations used for Paternity Test Cases 1 and 2 was that actual genetic data for the alleged father was used for Cases 1 and 2, but putative genetic data was used instead of actual genetic data for step 2 in Cases 3 through 8.
1) Theory
This example represents the standard trio case, which involves a mother, a child whose paternity is in question, and an alleged father (Figure 5). Based on Bayes’ Theorem, Essen-Moller [2,3] devised a formula for evaluating the probability of paternity in this standard paternity case. The probabilities calculated with the Essen-Moller formula are defined as follows:
X: probability (types observed | the hypothesis is that the tested man is the father)
Y: probability (types observed | the hypothesis is that the tested man is a random man)
The equation W=X/(X+Y) can transform DNA types into numerical expressions that represent the likelihood of paternity. In addition, the ratio X/Y was proposed to represent the paternity index (PI), where X/Y=PI [5,6]. Komatsu [7-9] also used Bayes’ Theorem to develop a formula for calculating the probability of paternity. The probabilities calculated with the Komatsu formula are defined as follows:
P1: probability (types observed|the hypothesis is that the tested person is the child of the father)
P2: probability (types observed|the hypothesis is that the tested person is the child of a random person)
In Komatsu’s methodology, the equation W=P1/(P1+P2) is used to express the likelihood of paternity, and the ratio P1/P2 is used to represent the paternity index (PI), where P1/P2=PI. Results of the Essen-Moller formulas, specifically values for the likelihood of paternity and the paternity index, are consistent with those of the Komatsu formulas. Here we used the Komatsu formulas, because they are suitable for constructing R scripts.
R script
In R script, likelihood of paternity for standard trio cases was assessed as follows:
In these cases, the genotypes of the mother, child, and alleged father were represented as [m1, m2], [c1, c2], and [f1, f2], respectively, where “m1” and “m2” represent both of the mother’s alleles of one gene, “c1” and “c2” represent both of the child’s alleles of that same gene, and “f1” and “f2” represent both of the alleged father’s alleles of that gene. The probability that c1 was inherited from the alleged father was represented by the term fc1, which was calculated with the following R script:
fc1< -{ifelse(f1==c1,1,0)+ifelse(f2==c1,1,0)}/2 [Script 1 1]
In R script, “< -” represents the definition sign. And “ifelse(f1==c1,1,0)” directs the return of 1 if f1 equals c1, or the return of 0 if f1 differs from c1 because “==” represents the equal sign.
The probability that c2 was inherited from the alleged father was represented by the term fc2.
fc2< -{ifelse(f1==c2,1,0)+ifelse(f2==c2,1,0)}/2 [Script 1 2]
The probability that c1 was inherited from the mother was represented by the term mc1.
mc1< -{ifelse(m1==c1,1,0)+ifelse(m2==c1,1,0)}/2 [Script 1 3]
The probability that c2 was inherited from the mother was represented by the term mc2.
mc2< -{ifelse(m1==c2,1,0)+ifelse(m2==c2,1,0)}/2 [Script 1 4]
Using these probabilities, P1 and P2 were calculated as follows:
P1< - (fc1*mc2+fc2*c1)/ifelse(c1==c2,2,1) [Script 1 5]
P2< -([gene frequency of c1]*mc2+[gene frequency of c2]*mc1) /ifelse(c1==c2,2,1) [Script 1 6]
1) Theory
In these cases the genotype of the mother was unavailable, but the genotypes of the child and the alleged father were available. Because one of the child’s alleles was inherited from an unspecified mother, mc1 and mc2 were set to the gene frequencies of c1 and c2, respectively.
In the following six scenarios (Paternity Test Cases 3 1 through 3 6), the alleged father’s genotype was unavailable, and his putative genotype was constructed from the genotype(s) of one or more of the following people in the following groupings: one or more of his ascendants (one or both of his parents and/or one or more of his siblings) or one or more of his descendants (one or more of his biological children or his wife and one or more of their biological children).
1) Theory
The alleged father’s putative genotype was constructed based on the genotypes of his mother and father. His father’s genotype and his mother’s genotype were represented as [F1, F2] and [M1, M2], respectively. We could infer that the genotype of the alleged father was either [F1, M1], [F1, M2], [F2, M1], or [F2, M2].
1) Theory
The alleged father’s putative genotype was constructed based on the genotype of only one of his parents. The genotype of this one parent was represented as [P1, P2], and x can represent any allele. We could infer the genotype of the alleged father was either [P1, x] or [P2, x].
1) Theory
The alleged father’s putative genotype was constructed based on the genotype of one or more of his siblings and that of one of his parents. The putative genotype of the alleged father’s remaining parent was constructed based on the patterns listed in Table 2. We used Bayes’ Theorem to calculate a conditional probability for the putative genotype that was constructed for his remaining parent. The genotypes of one of his parents and anywhere from one to five siblings were represented as [PA1, PA2] and [S1, S2] (which represents [S1,S2]1 or some sequential combination of [S1,S2]1, [S1,S2]2, [S1,S2]3, [S1,S2]4, and [S1,S2]5). The putative genotype of his remaining parent is [PB1, PB2]. Given [S1, S2], the posterior probability of [PA1, PA2] and [PB1, PB2]1 was calculated as follows:
 [Formula 3 3]
[Formula 3 3]
2) R script
In the R script we devised, the posterior probability of [PA1, PA2] and [PB1,PB2]1 was assessed as follows: The probability that S1 was inherited from one of the alleged father’s parents (genotype: [PA1, PA2]) was represented by the term pas1.
pas1< -{ifelse(PA1==S1,1,0)+ifelse(PA2==S1,1,0)}/2 [Script 3 3 1]
The probability that S2 was inherited from one of the alleged father’s parents (genotype: [PA1, PA2]) was represented by the term pas2.
pas2< -{ifelse(PA1==S2,1,0)+ifelse(PA2==S2,1,0)}/2 [Script 3 3 2]
The probability that S1 was inherited from his remaining parent (genotype: [PB1, PB2]) was represented by the term pbs1.
pbs1< -{ifelse(PB1==S1,1,0)+ifelse(PB2==S1,1,0)}/2 [Script 3 3 3]
The probability that S2 was inherited from his remaining parent (genotype: [PB1, PB2]) was represented by the term pbs2.
pbs2< -{ifelse(PB1==S2,1,0)+ifelse(PB2==S2,1,0)}/2 [Script 3 3 4]
The posterior probability of [PA1, PA2] and [PB1, PB2]1 was represented by the term piba1, and calculated with the following scripts:
pabs1< -(pas1*pbs2+pas2*pbs1)/ifelse(S1==S2,2,1) [Script 3 3 5]
piba1< -pab1s1*pab1s2*pab1s3*pab1s4*pab1s5*[frequency of [PB1, PB2]1]/Σpabjs1*pabjs2*pabjs3*pabjs4*pabjs5*[frequency of [PB1, PB2]j] [Script 3 3 6]
In most cases, genotype frequency of [PB1, PB2] was calculated with following formulas.
[PB1, PB2] is homozygous:
1*[allele frequency of PB1]*[allele frequency of PB2]
[PB1, PB2] is heterozygous:
2*[allele frequency of PB1]*[allele frequency of PB2]
The child whose paternity was unknown had the genotype [c1, c2]. In addition, fc1, which was defined as the probability that c1 was inherited from the alleged father, was calculated with the following R script:
fc1=(sum(c(PA1,PA2,PB1,PB2)==c1)/4)*P([PA1,PA2], [PB1,PB2]1|[S1,S2]) [Script 3 3 7]
The R script, sum(c(PA1,PA2,PB1,PB2)==c1), indicated the number of alleles that equaled c1.
1) Theory
The alleged father’s putative genotype was constructed based on the genotype of one or more of his siblings. The putative genotypes of the alleged father’s parents were constructed based on the patterns listed in Table 3. The genotypes of one to five siblings were represented as [S1, S2] (which represents [S1,S2]1 or some sequential combination of [S1,S2]1, [S1,S2]2, [S1,S2]3, [S1,S2]4, and [S1,S2]5). Putative genotypes of the alleged father’s parents are [PA1, PA2] and [PB1, PB2]. Given [S1, S2], the posterior probability of [PA1, PA2]1 and [PB1, PB2]1 was calculated as follows:
 [Formula 3 4]
[Formula 3 4]
The basic structure of the R script was identical to [Script 3 3 7].
1) Theory
The alleged father’s putative genotype was constructed based on the genotypes of his wife and their biological children. The putative genotype of the alleged father was constructed based on the patterns listed in Table 2. The genotype of his wife and those of their biological children were represented as [W1, W2] for the wife and [C1, C2] (which represents [C1,C2]1 or some sequential combination of [C1,C2]1, [C1,C2]2, [C1,C2]3, [C1,C2]4, and [C1,C2]5). The putative genotype of the alleged father was represented as [F1, F2]. Given [C1, C2], the posterior probability of [F1, F2]1 and [W1, W2] was calculated as follows:
 [Formula 3 5]
[Formula 3 5]
The basic structure of the R script was identical to [Script 3 3 6].
1) Theory
The alleged father’s putative genotype was constructed from the genotype or genotypes of one or more of his biological children. The putative genotypes of the alleged father and his wife were constructed based on the patterns listed in Table 3. The genotypes of one or more of the alleged father’s biological children were represented as [C1, C2] (which represents [C1,C2]1 or some sequential combination of [C1,C2]1, [C1,C2]2, [C1,C2]3, [C1,C2]4, and [C1,C2]5). The putative genotypes of the alleged father and his wife were represented as [F1, F2] and [W1, W2], respectively. Given [C1, C2], the posterior probability of [F1, F2]1 and [W1, W2]1 was calculated as follows:
 [Formula 3 6 1]
[Formula 3 6 1]
The basic structure of R script was identical to [Script 3 3 6]. From this posterior probability, the probability of the alleged father’s putative genotype was calculated as follows:
 [Formula 3 6 2]
[Formula 3 6 2]
In the following four scenarios (Paternity Test Cases 4 1 through 4 4), the alleged father’s putative genotype was constructed based on the genotypes of his parents, his siblings, his wife, and one or more of his biological children, or on the genotypes of one or some combination of these relatives.
1) Theory
The alleged father’s putative genotype was constructed based on the genotypes of his parents, his wife, and one or more of his biological children. The putative genotype of the alleged father was estimated from the genotypes of his parents as described in Paternity Test Case 3 1. Given the genotype of his biological children, the posterior probability of the alleged father’s putative genotype was calculated via [Formula 3 5].
1) Theory
The alleged father’s putative genotype was constructed based on the genotype of one of his parents and those of his wife and one or more of his biological children. The putative genotype of the alleged father was estimated from the genotype of one of his parents as described in Paternity Test Case 3 2. Given the genotype of his biological children, the posterior probability of the alleged father’s putative genotype was calculated via [Formula 3 5].
1) Theory
The alleged father’s putative genotype was constructed based on the genotype of one of his parents and those of his siblings, his wife, and his biological children. The putative genotype of his remaining parent was estimated from the genotype of his other parent and his siblings as described in Paternity Test Case 3 3. Given the genotype of his biological children, the posterior probability of the alleged father’s putative genotype was calculated via [Formula 3 5].
1) Theory
The alleged father’s putative genotype was constructed based on the genotype of one of his parents and those of his siblings, his wife, and his biological children. The putative genotype of his remaining parent was estimated from the genotype of his other parent and his siblings as described in Paternity Test Case 3 3. Given the genotype of his biological children, the posterior probability of the alleged father’s putative genotype was calculated via [Formula 3 5].
In the following three groups of scenarios (Paternity Test Cases 5 1 through 5 3), the alleged father’s putative genotype was constructed based on the genotypes from his parents, his siblings, his biological children or some combination of these relatives.
1) Theory
The alleged father’s putative genotype was constructed based on the genotypes of his parents and his biological children. The genotypes of the alleged father’s parents were used to construct his putative genotype as described in Paternity Test Case 3 1; similarly, [Formula 3 6 2] was used to construct the alleged father’s putative genotype from the genotypes of his biological children. Thus, two putative genotypes were constructed for the alleged father, one based on his parents’ genotypes and another based on his biological children’s genotypes; these putative genotypes were represented as [UF1, UF2] and [LF1, LF2], respectively. Given [LF1, LF2], the posterior probability of [UF1, UF2]1 was calculated as follows:
 [Formula 5 1]
[Formula 5 1]
2) R script
P([LF1,LF2]k| [UF1,UF2]1) was assessed with the following R script:
UL< -{(ifelse(UF1==LF1,1,0)*ifelse(UF2==LF2,1,0)*[posterior probability of [LF1,LF2]]+ifelse(UF1==LF2,1,0) *ifelse(UF2==LF1,1,0)* [posterior probability of [LF1,LF2]])/ifelse(UF1==UF2,2,1)} [Script 5 1 1]
Therefore, P([UF1, UF2]1|[LF1,LF2]) was calculated as follows:
ulf1< -ΣULk* [posterior probability of [UF1,UF2]1]/ΣΣULk* [posterior probability of [UF1,UF2]j] [Script 5 1 2]
1) Theory
Two separate putative genotypes were constructed for the alleged father; one was based on the genotype of one of his parents, and the other on genotypes of his biological children. The putative genotype that was based on one of the alleged father’s parents was constructed as described in Paternity Test Case 3 2; the putative genotype that was based on the genotypes of the alleged father’s biological children was determined with [Formula 3 6 2]. Given the alleged father’s putative genotypes from his biological children, the posterior probability of the alleged father’s putative genotypes from one of his parents was calculated by [Formula 5 1].
1) Theory
Two separate putative genotypes for the alleged father were constructed; one putative genotype was based on the genotypes of one of his parents and those of one or more of his siblings; the other was based on the genotypes of one or more of his biological children. The putative genotype based on the genotype of one of the alleged father’s parents and his siblings was constructed with [Formula 3 3]; the putative genotype based on the genotype of his biological children was constructed with [Formula 3 6 2]. Given the alleged father’s putative genotype that was based on his biological children, the posterior probability of the alleged father’s putative genotype from one of his parents and his siblings was calculated with [Formula 5 1].
1) Theory
In the following three groups of scenarios (Paternity Test Cases 6, 7, 8), putative genotypes were constructed for the alleged father based on the genotypes of his siblings and those of his biological children. The putative genotype based on his siblings’ genotypes was constructed with [Formula 3 4]; the putative genotype based on the biological children’s genotypes was constructed with [Formula 3 6 2]. Given the alleged father’s putative genotype that was based on the genotypes of his biological children, the posterior probability of the alleged father’s putative genotype from his siblings was calculated with [Formula 5 1].
Fundamental operations of R are described in commercially available books [24-26], and on websites [23]. R can be downloaded from mirror sites, which can be found all over the world. In Figure 5, the script for the standard trio case (Paternity Test Case 1) is shown. The term x represents an individual allele and can expressed as an Arabic numeral between 0 and 20. The term ‘z’ represented the frequency of a particular allele, which corresponded to the number of x by turns. Genotypes were then expressed by Arabic numeral in term x. Since R is mathematical software, alleles need to be expressed in Arabic numerals. For example, it was impossible analyze a genotype that was represented as [geneA, genea]. In such cases, “geneA ” was replaced with “1” in term x and “ genea” was replaced with “2”. Moreover, the genotypes had to be listed in ascending order; for example, [2, 4] was suitable, but [4, 2] was not. For any allele that was not available, “0” was used in term x; for example, the genotype of sibling 5 was unavailable; therefore, this genotype was expressed as [0, 0]. In addition, “0” in term x corresponds to “1” in term z. The likelihood of paternity and the paternity index were then calculated when the terms “probability” and “ratio”, respectively, were entered.
Computer programs designed for the analysis of pedigrees can be classified into two categories. The programs in the first category employ the distinctive pull-down menus [10,12,13,18,19]. Those in the second category use common software applications, such as Microsoft Excel [11], and the end users must perform manual operations, such as general computer manipulations and spreadsheet selections, to calculate the probability of paternity with these programs
Programs with pull-down menus make operation easy for most investigators because only inputs and clicks of DNA types and gene frequencies are required for calculation of the likelihood of paternity or of a paternity index. In other words, most users can get results without thorough knowledge of paternity testing. When describing the theories behind the calculations necessary to evaluate complicated or incomplete pedigrees, the papers that describe programs with pull-down menus provide only minimal and generalized formulas. These descriptions are accurate, but we believe that many forensic researchers do not have the background necessary to understand them. In actuality, the pedigrees and the cells into which DNA typing information is entered are fixed in these types of programs. Therefore, changes and modifications to the system are difficult, and flexible extensions cannot be easily implemented by an individual researcher. Moreover, these types of programs are extremely expensive; therefore, only a small number of institutions can afford them, and only researchers at those institutions can examine pedigrees as complicated as the ones described here. Some researchers say that handy computer programs that can generate results automatically via pull-down menus are useful for complicated paternity cases. But in our opinion, an understanding of the calculations and the theory used to analyze complex pedigrees is important and necessary for further development of calculation systems and programs. Detailed explanations that are understandable for every researcher are required. Presentations of both the family trees and the concrete formulas would be essential for understanding calculations of necessary for assessing complex pedigrees. The lack of papers accessible to such beginners and non-mathematicians prompted the present study.
Pedigree software applications that require more manual operation by the user are more flexible and can be used for more applications; they also provide valuable information about the calculations. In such software applications, structures and formulas for pedigree analyses are easily accessible. Viewed in this light, the Aoki paternity spreadsheet [11] remains innovative and promising. It was constructed in Excel (Microsoft, Redmond, WA); consequently, the detailed mathematical or genetic hypotheses necessary to analyze complex pedigrees are easily accessible to researchers. Therefore, investigators can study the theory and easily modify programs. Increasingly, R is becoming the standard programming language for biostatistics [24, 25], and it is distributed free of charge. Given these circumstances, we created paternity testing scripts with R. We also confirmed that these scripts generated the same values for the likelihood of paternity and the paternity index as did the Aoki paternity spreadsheet [11]. Since some R scripts involve very complex computations, integrations of contiguous pedigrees are difficult. In the system described here, the scripts were constructed for each case; this strategy should greatly facilitate the understanding of the calculations used for complex cases. R is an interactive program; therefore, we described the formulas in an orderly fashion. Investigators that lack a programming background should be able to understand the calculations necessary for the analysis of complicated cases by reading these scripts. In addition, advanced computer literacy is not required for writing R scripts. Modifications to the R scripts, such as changes in the pedigrees and or changes to the number of relatives, should be relatively easy to implement by copying and pasting existing formulas. Each of the R scripts presented here is an open-source tool, and we are happy to share them with any researcher (https://www. geocities.jp/mmtakamiya/index.html). Please note these scripts are distributed under the GPL license version 3. Although each described here relies on autosomal markers at a single locus, practical genotyping could be performed at multiple loci on different chromosomes. Therefore, the following formula must be used to calculate joint probabilities.
 [Formula 3 6 2]
[Formula 3 6 2]
This study describes fundamental R formulas that can be used for paternity testing. By acquiring, learning, and using these scripts, any interested researcher can develop calculation systems of their own.
Computer programs to assess complex cases of undetermined paternity are available, but in general, molecular genetic data for the alleged father is unavailable in these complicated cases. Unfortunately, the reports describing the existing programs provide only minimal and generalized formulas, and most forensic researchers have difficulty understanding such reports. Therefore, more detailed and understandable explanations of the software programs used in paternity determination should be more readily available to forensics researchers.
R is an increasingly popular programming language that is used for mathematical calculations and statistical analyses; moreover, it is used by a growing number of researchers in bioinformatics and biostatistics. This paper describes concrete and detailed calculations and R scripts that can be used for paternity testing; these descriptions would aid any researcher attempting to efficiently understand the calculations used to assess complicated paternity cases. Moreover, individual researchers can develop paternity calculation systems of their own by acquiring, learning, and using these scripts.
This study was supported by JSPS KAKENHI Grant Number 24790641.
| Paternity Test Case 1: Test involving a mother, child, and alleged father | |
| Paternity Test Case 2: Test involving a child and alleged father | |
Paternity Test Cases 3 through 8 are tests involving an alleged father whose genotype is unavailable, a mother and a child. |
|
| Paternity Test Case 3: The genotype of the alleged father was constructed based on genetic data from his parents and his siblings or from his wife and their biological children. | |
| Paternity Test Case 3 1: | The genotype was constructed based on genetic data from the alleged father’s parents. |
| Paternity Test Case 3 2: | The genotype was constructed based on genetic data from one of alleged father’s parents. |
| Paternity Test Case 3 3: | The genotype was constructed based on genetic data from one of alleged father’s parents and his siblings. |
| Paternity Test Case 3 4: | The genotype was constructed based on genetic data from the alleged father’s siblings. |
| Paternity Test Case 3 5: | The genotype was constructed based on genetic data from the alleged father’s wife and their biological children. |
| Paternity Test Case 3 6: | The genotype was constructed based on genetic data from the alleged father’s biological children. |
| Paternity Test Case 4: The genotype of the alleged father was constructed based on genetic data from his parents, his siblings, his wife, and their biological children. | |
| Paternity Test Case 4 1: | The genotype was constructed based on genetic data from the alleged father’s parents, his wife, and their biological children. |
| Paternity Test Case 4 2: | The genotype was constructed based on genetic data from one of alleged father’s parents, his wife, and their biological children. |
| Paternity Test Case 4 3: | The genotype was constructed based on genetic data from one of alleged father’s parents, his siblings, his wife, and their biological children. |
| Paternity Test Case 4 4: | The genotype was constructed based on genetic data from the alleged father’s siblings, his wife, and their biological children. |
| Paternity Test Case 5: The genotype of the alleged father was constructed based on genetic data from his parents, his siblings, and his biological children. | |
| Paternity Test Case 5 1: | The genotype was constructed based on genetic data from the alleged father’s parents and his biological children. |
| Paternity Test Case 5 2: | The genotype was constructed based on genetic data from one of alleged father’s parents and his biological children. |
| Paternity Test Case 5 3: | The genotype was constructed based on genetic data from one of alleged father’s parents, his siblings, and his biological children. |
| Paternity Test Case 6: The genotype of the alleged father was constructed based on genetic data from his siblings with different genotypes and his biological children. | |
| Paternity Test Case 7: The genotype of the alleged father was constructed based on genetic data from his siblings with one common homozygous genotype, and his biological children. | |
| Paternity Test Case 8: The genotype of the alleged father was constructed based on genetic data from his siblings with one common heterozygous genotype, and his biological children. | |
Paternity Test Case 7: Genotypes of 5 siblings (S1: [A, A], S2: [A, A], S3: [A, A], S4: [A, A], S5: [A, A])
Paternity Test Case 8: Genotypes of 5 siblings (S1: [A, B], S2: [A, B], S3: [A, B], S4: [A, B], S5: [A, B])
Table 1: Contents of the scripts
Genetic information from parent and child |
|||
| Genotype of the parent | Genotype of the child | Number of alleles in common between parent and child | |
| Pattern 1 | heterozygous | heterozygous | 1 |
| Pattern 2 | heterozygous | heterozygous | 2 |
| Pattern 3 | homozygous | homozygous | 1 |
| Pattern 4 | homozygous | heterozygous | 1 |
| Pattern 5 | heterozygous | homozygous | 1 |
Pattern 1: Genotypes of parent [A, B] and child [A, C]
Pattern 2: Genotypes of parent [A, B] and child [A, B]
Table 2: Classification of a parent and child for constructing the genotype of the remaining parent
Genetic information from children |
|||
| Number of homozygous genotypes among children | Number of heterozygous genotypes among children | Number of alleles among children | |
Pattern 1 |
1 |
0 |
1 |
Pattern 2 |
0 |
1 |
2 |
Pattern 3 |
1 |
1 |
2 |
Pattern 4 |
0 |
2 |
3 |
Pattern 5 |
0 |
3 |
3 |
Pattern 6 |
0 |
2 |
4 |
Pattern 7 |
2 |
0 |
2 |
Pattern 8 |
1 |
>0 |
3 |
Pattern 9 |
0 |
>2 |
4 |
Pattern 1: Genotypes of 5 children (C1: [A, A], C2: [A, A], C3: [A, A], C4: [A, A], C5: [A, A])
Pattern 2: Genotypes of 5 children (C1: [A, B], C2: [A, B], C3: [A, B], C4: [A, B], C5: [A, B])
Table 3: Classification of children for constructing genotypes of parents
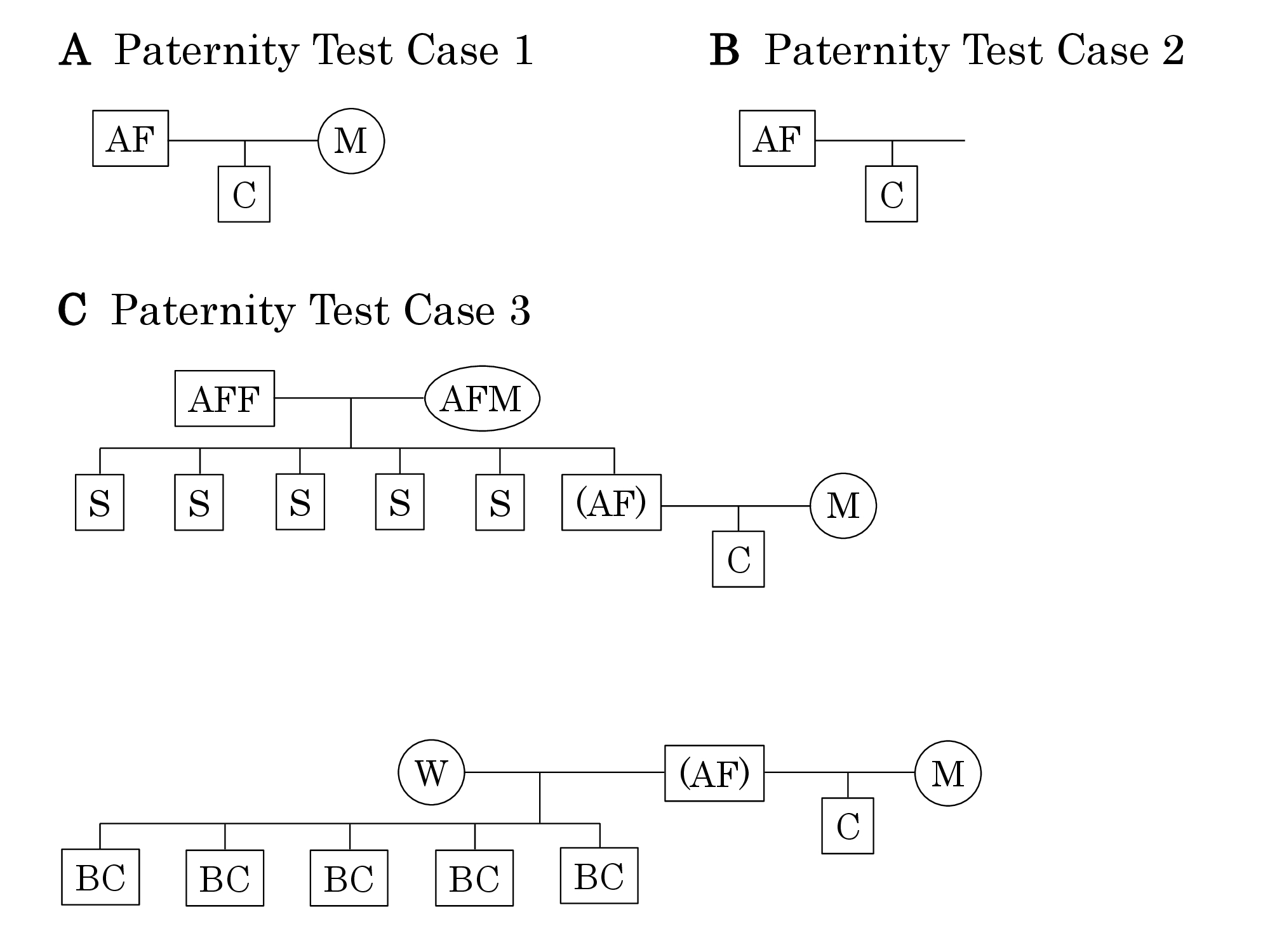 |
| Figure 1: Pedigrees that represent the scenarios described in Paternity Test Case 1 (A), Paternity Test Case 2 (B), and Paternity Test Case 3 (C): AF: alleged father, (AF): alleged father, for whom no DNA genotyping is available, M: mother, C: child, AFF: alleged father’s father, AFM: Alleged father’s mother, S: alleged father’s sibling, W: alleged father’s wife, BC: alleged father’s biological child. |
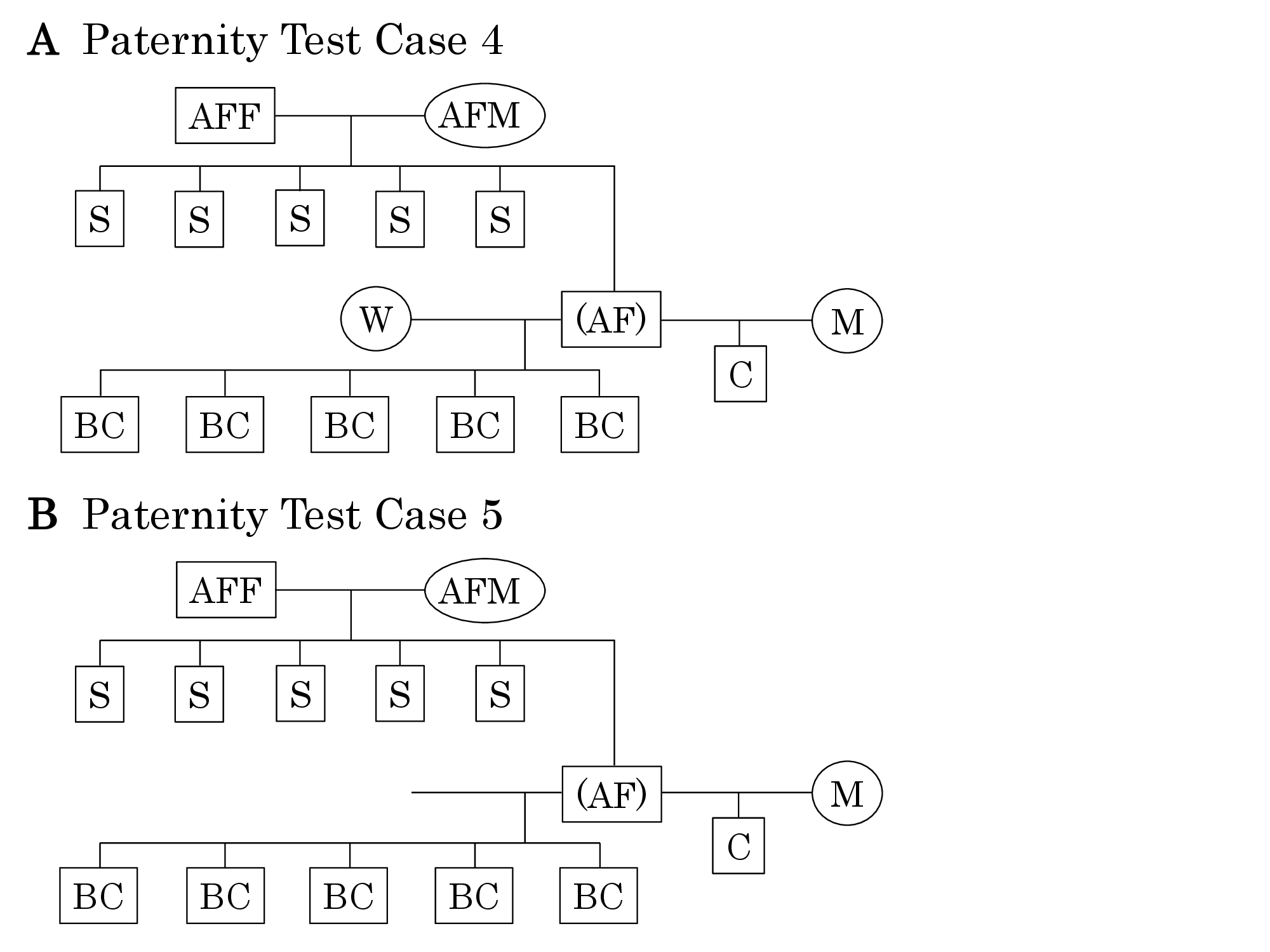 |
| Figure 2: Pedigrees that represent the scenarios described in Paternity Test Case 4 (A) and Paternity Test Case 5 (B). Explanatory notes are the same as those for Figure 1. |
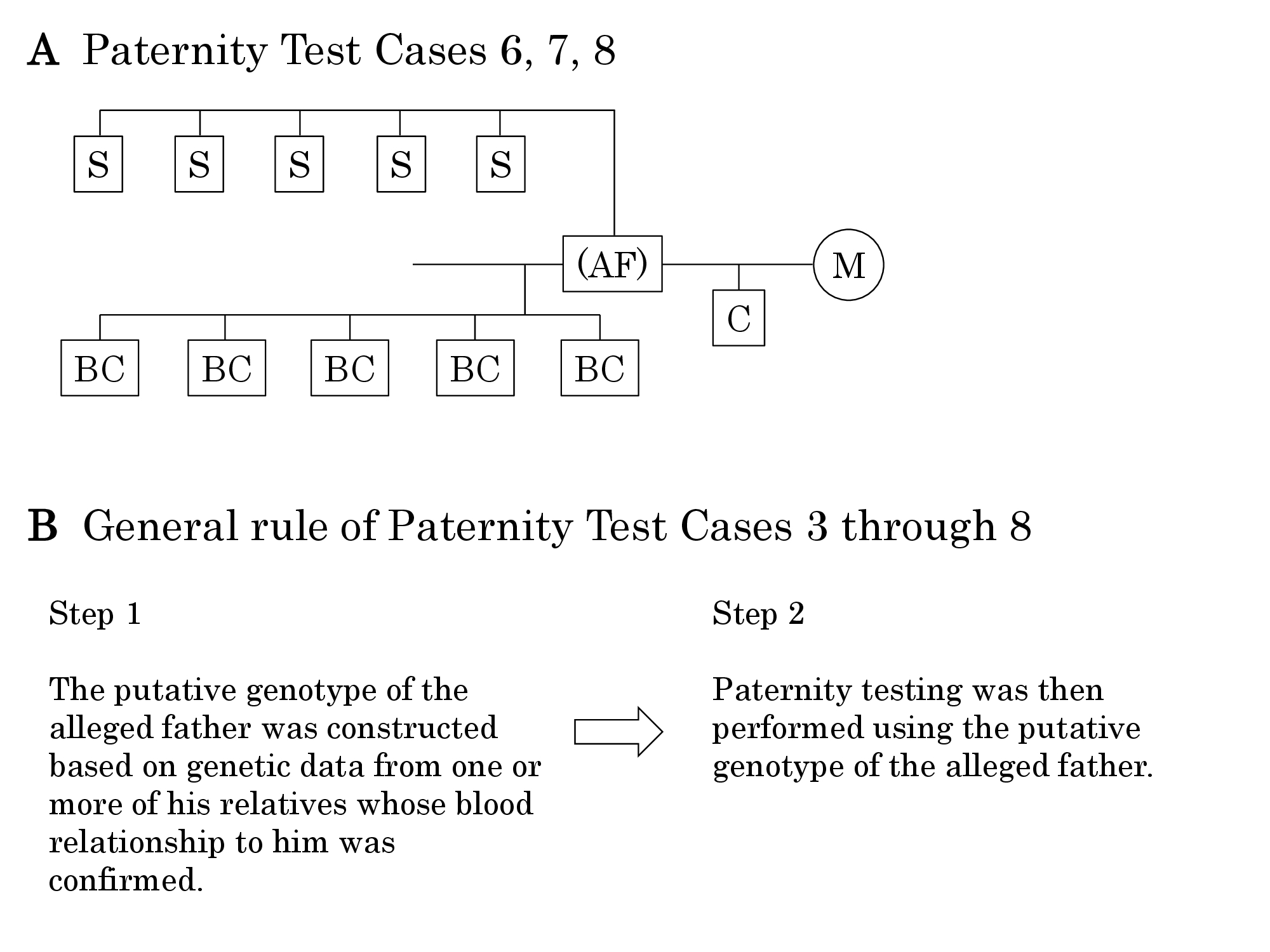 |
| Figure 3: The pedigree that represents the scenarios described in Paternity Test Cases 6 through 8 (A). Explanatory notes are the same as those for Figure 1. The General Rule (B) describes the two overarching steps that were used to assess paternity in Paternity Test Cases 3 through 8. |
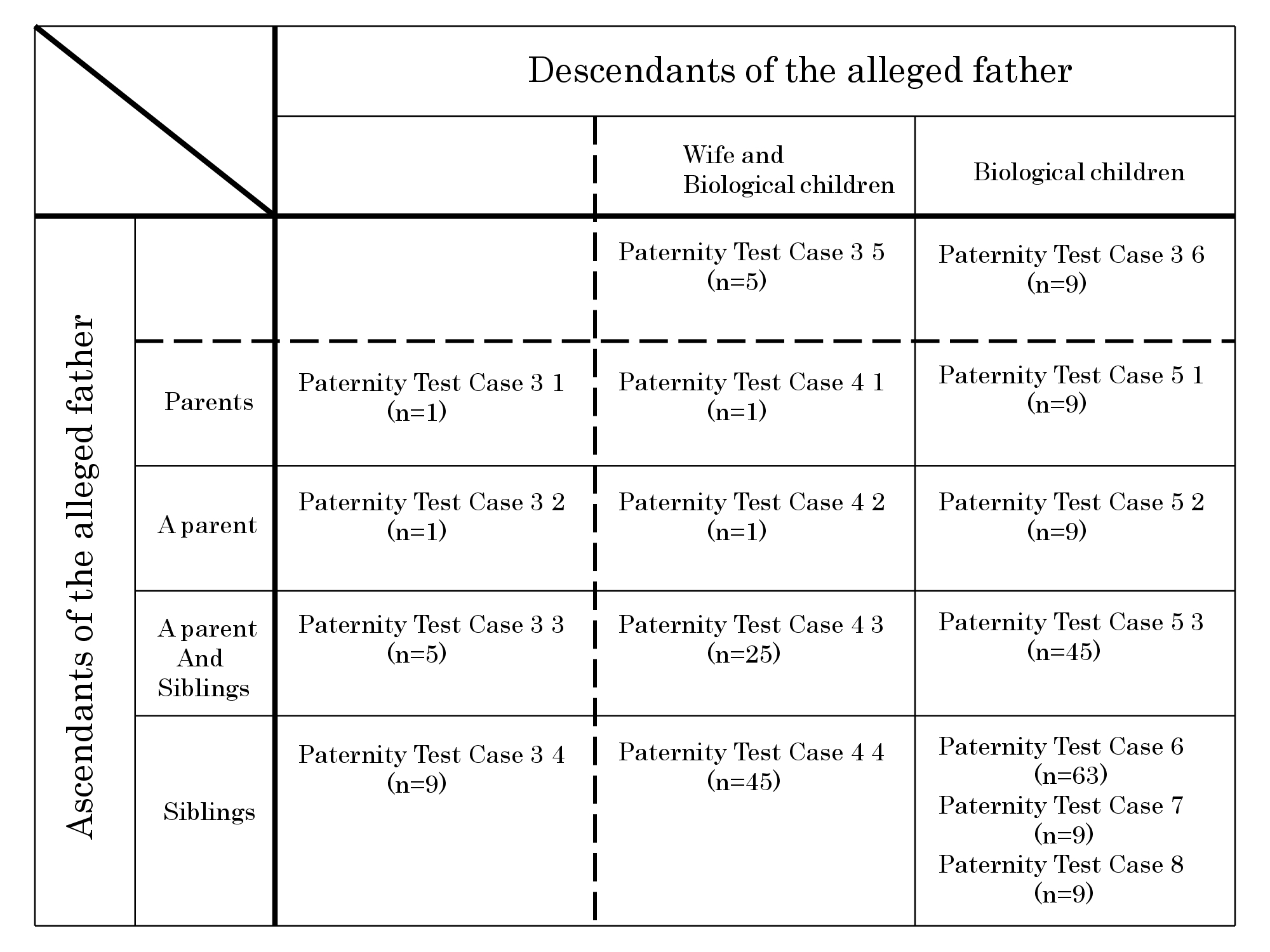 |
| Figure 4: Relationships among scripts used for Paternity Test Cases 3 through 8. Cells outside of broken lines indicate tests that were based on genotypes of ascendants or descendants of the alleged father; the cells inside of broken lines indicate tests that were based on genotypes of ascendants and descendants. The number of the scripts used for each paternity testing is also shown in parentheses. |
 |
| Figure 5: Script used for analysis of the standard trio case, which is the scenario described in Paternity Test Case 1. The genotypes of mother, child, and alleged father are represented as [2, 4], [2, 4], and [2, 4], respectively. The function of each code is as follows; < -: definition, ==: equal, ifelse: conditional element selection, data.frame: store of data tables, subset: conditional element selection. In addition, the definition of each formula is shown in “A. Paternity Test Case 1” and the ”Instruction for users” in the Materials and methods section. |






































